1.3 Le seuil de percolation
Pendant longtemps, la recherche s'est focalisée sur l'étude du seuil de percolation (percolation threshold).
En conséquence, de nombreuses méthodes on été développées pour calculer ou estimer la valeur de pc. Après une brève
définition de la notion de seuil de percolation (§ 1.3.1), les problèmes relatifs à la
dimension finie des réseaux étudiés seront exposés (§ 1.3.2). Ensuite, plusieurs méthodes utilisées
pour déterminer la valeur du seuil critique seront présentées avant d'énoncer les résultats obtenus sur divers réseaux
(§ 1.3.3). Enfin, la question du nombre d'amas infini simultanément envisageables, sur un réseau, sera
abordée (§ 1.3.4).
1.3.1 Définition
Après une définition du seuil de percolation dans les modèles de percolation de sites et de liens, la notion sera
présentée dans le problème de percolation mixte.
Percolation de sites, percolation de liens
Au sein d'un réseau dans lequel les sites (ou les liens) sont actifs avec une probabilité p et
inactifs avec une probabilité q = 1 – p, le seuil de percolation pc se définit comme la
concentration p à laquelle un amas de taille infinie apparaît dans un réseau de taille
infinie (Clerc et alii, 1983, p. 17). Pour tout p > pc, une chaîne s'étend d'un
côté à l'autre du système alors que pour p < pc, il n'existe pas de « chemin » de ce type. La
figure 1.23 (b) montre l'apparition de l'amas percolant à p = pc dans un
réseau carré de sites.
Figure 1.23: Exemple de percolation sur un réseau carré de sites pour différents p
| (a) (p = 0,4) |
(b) (p = 0,6 ~ pc ) |
(c) (p = 0,8) |
 |
 |
 |
| (25 × 25 sites) |
Au fur et à mesure que la proportion d'activité p s'accroît, la taille des amas augmente mais
reste de taille finie (figure 1.23 (a)). À partir d'une valeur déterministe,
on observe l'apparition d'un amas qui joint les bords opposés
(figure 1.23 (b)). Cet amas est l'amas percolant et la valeur de cette
probabilité critique correspond au seuil de percolation (pc ~ 0,5928 pour un
réseau carré de sites). Les sites éléments de l'amas infini sont représentés en noir pour mettre en
relief la jonction des côtés opposés. Les sites en gris sont les sites actifs distincts de l'amas
percolant. On constate que le nombre de sites séparés de l'amas infini diminue lorsque p augmente
(figure 1.23 (c)).
La figure 1.24 illustre l'apparition de l'amas percolant dans un réseau carré
de liens (pc = 1/2 pour un réseau carré de liens).
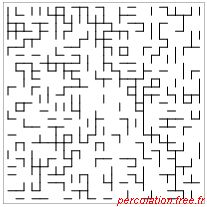
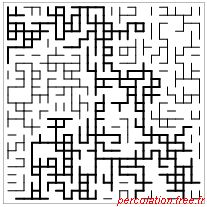
Figure 1.24: Exemple de percolation sur un réseau carré de liens pour différents p
| (a) (p = 0,35) |
(b) (p = 0,5 = pc) |
(c) (p = 0,65) |
 |
 |
 |
| (25 × 25 sites) |
L'amas infini est représenté en gras lorsqu'il existe. On retrouve la même évolution que pour le
problème de sites : lorsque p < pc les amas sont de taille finie et lorsque p > pc un amas
reliant les bords opposés apparaît.
Dans la théorie de la percolation, l'existence du seuil est fondamental. Cette valeur critique se
caractérise par (Kesten, 1987, p. 1233) :
| P(p) |
ì
í
î |
| = 0 |
si |
p < pc |
| > 0 |
si |
p > pc |
|
|
pc = sup{p:P(p) = 0}
Dans les modèles de percolation de sites et de percolation de liens, on obtient intuitivement les
propriétés suivantes (Kesten, 1987, p. 1232) :
-
la probabilité de percolation est nulle si le taux d'activité est nul : P(0) = 0 ;
- la probabilité de percolation est certaine si le taux d'activité est de 100 % : P(1) = 1 ;
- la probabilité de percolation est une fonction non-décroissante de p : p ® P(p) > 0.
En conséquence, la forme générale de la fonction de probabilité de percolation P(p) est supposée
évoluer selon le schéma de la figure 1.25.
Figure 1.25: Probabilité de percolation P(p)
 |
| Source : Kesten (1987), p. 1233 |
De la sorte, la probabilité de percolation P(p) est une fonction continue de p avec
vraisemblablement une exception au seuil de percolation pc (Grimmett, 1989, p. 13). En fait, la
possibilité d'une discontinuité n'est pas exclue pour des dimensions d > 3.
Percolation mixte
Le problème de percolation mixte génère une dynamique plus complexe car le seuil de percolation
combine deux paramètres : probabilité d'activité des sites ps et probabilité d'activité des
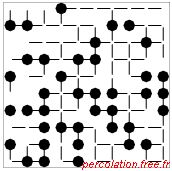
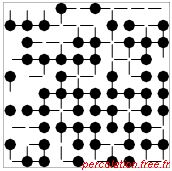
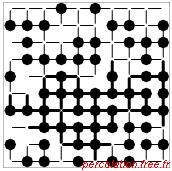
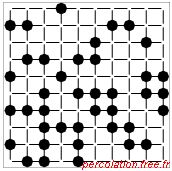
liens pb. Sur la figure 1.26, seize situations sont représentées afin de
distinguer les effets des variations de ps et pb.
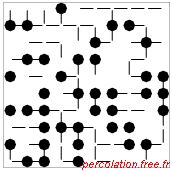
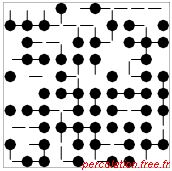
Figure 1.26: Exemple de percolation sur un réseau carré mixte pour différents p
| (a) |
(b) |
(c) |
(d)* |
| (ps = 0,4 ; pb = 0,4) |
(ps = 0,6 ; pb = 0,4) |
(ps = 0,8 ; pb = 0,4) |
(ps = 1,0 ; pb = 0,4) |
 |
 |
 |
 |
| (e) |
(f) |
(g)* |
(h)* |
| (ps = 0,4 ; pb = 0,6) |
(ps = 0,6 ; pb = 0,6) |
(ps = 0,8 ; pb = 0,6) |
(ps = 1,0 ; pb = 0,6) |
 |
 |
 |
 |
| (i) |
(j)* |
(k)* |
(l)* |
| (ps = 0,4 ; pb = 0,8) |
(ps = 0,6 ; pb = 0,8) |
(ps = 0,8 ; pb = 0,8) |
(ps = 1,0 ; pb = 0,8) |
 |
 |
 |
 |
| (m) |
(n)* |
(o)* |
(p)* |
| (ps = 0,4 ; pb = 1,0) |
(ps = 0,6 ; pb = 1,0) |
(ps = 0,8 ; pb = 1,0) |
(ps = 1,0 ; pb = 1,0) |
 |
 |
 |
 |
| * : présence d'un amas percolant |
(10 × 10 sites) |
Sur chaque ligne, la situation des liens est donnée : pb est constant et ps varie. Sur chaque
colonne, la situation des sites est fixe : ps est constant et pb varie. Pour comparer les
effets relatifs des deux paramètres, les variations par ligne et par colonne se font par tranche de
20 %. Sur chaque figure l'amas percolant est représenté en gras et une étoile (*) souligne
sa présence à côté de l'étiquette du graphique.
On constate tout d'abord, que l'augmentation conjointe de ps et pb conduit plus ou moins
rapidement à l'apparition d'un amas percolant. Si toutes choses égales par ailleurs, on accroît la
valeur d'un des deux paramètres seulement, il y a généralement émergence d'un amas infini mais ce
n'est pas toujours le cas. Dans les situations (a), (e) et (i) par exemple, quelle que soit
l'augmentation d'activité des liens, il n'y a pas percolation. Pour faire un parallèle avec la
biologie, l'activité des sites peut être qualifiée de « facteur limitant »9.
De façon générale, la figure 1.26 évoque la question de l'importance relative
des sites et des liens. Les figures (d) et (m) sont définies respectivement par (ps = 1,0 ;
pb = 0,4) et (ps = 0,4 ; pb = 1,0). Bien que leurs combinaisons soient symétriques, on constate
que la figure (d) est percolante alors que la figure (m) ne l'est pas. S'il n'y a pas percolation
dans la configuration (m), c'est que le taux d'activité des sites est trop faible et qu'il joue le
rôle de facteur limitant. Intuitivement, cette configuration particulière est révélatrice de
l'importance relative des sites par rapport aux liens. En effet, pour un seul site supprimé dans
une structure carrée, jusqu'à quatre liens actifs peuvent êtres désolidarisés. Pour un
lien éliminé, ce sont au maximum deux sites actifs qui se retrouvent déconnectés. Dans des
situations singulières (pb très faible), l'activité des liens peut elle aussi apparaître comme
facteur limitant, mais de façon générale le taux d'activité des sites est plus influent que le taux
d'activité des liens dans les modèles de percolation mixte. Ainsi, le seuil de percolation de liens
est inférieur ou égal au seuil de percolation de sites pour un graphe donné10.
L'un des intérêts majeurs du modèle mixte par rapport aux modèles élémentaires de sites et de liens
est de proposer de nouvelles solutions pour influencer la percolation du système. Dans la situation
(b) par exemple, trois possibilités sont offertes pour atteindre le seuil critique :
-
augmenter fortement l'activité des sites : D ps = + 0,4 (figure (d)) ;
- augmenter fortement l'activité des liens : D pb = + 0,4 (figure (j)) ;
- augmenter moyennement l'activité des sites et celle des liens : D ps = D ps = + 0,2
(figure (g)).
Ces trois solutions sont équivalentes du point de vue de l'existence de
l'amas percolant, mais les propriétés de l'amas sont très différentes d'une situation à l'autre. En
effet, la forme, la structure et la répartition de l'amas infini sur le réseau se distinguent
fortement. C'est la nature du problème envisagé qui détermine alors quelle solution est la plus
efficace.
Soit P(ps, pb) la probabilité de percolation dans un graphe G donné avec respectivement
ps et pb les probabilités d'activité des sites et des liens. Certaines propriétés
caractérisent cette probabilité de percolation (Hammersley et Welsh, 1980, p. 596) :
-
si au moins l'un des taux d'activité est nul, la probabilité de percolation est nulle :
P(0, 0) = P(1, 0) = P(0, 1) = 0 ;
- si les deux taux d'activités sont de 100 %, la probabilité de percolation est certaine :
P(1, 1) = 1 ;
- la probabilité de percolation est une fonction non-décroissante de ps et pb :
ps, pb ® P(ps, pb) > 0.
Ainsi, le carré unitaire dans le plan (ps, pb) se décompose en deux zones A et B
(Hammersley et Welsh, 1980, p. 596). Dans la zone A, la probabilité de percolation est nulle.
Dans la zone B, la probabilité de percolation est positive. Les deux zones sont séparées par une
courbe critique : la ligne de transition.
Soient deux graphes G1 et G2 de connexité moyenne différente11. Sur la
figure 1.27, les deux zones A et B sont séparées par une ligne de
transition T1 pour le graphe G1 et T2 pour le graphe G2.
Figure 1.27: Probabilité de percolation dans un modèle mixte P(ps, pb)
 |
| Source : adapté de Clerc et alii (1983), p. 11 |
Dans la zone A, les amas sont de taille finie car la probabilité de percolation est nulle. Dans la zone B, la
présence d'un amas de taille infinie est possible car la probabilité de percolation est positive12. La position de la ligne de
transition dépend des caractéristiques du graphe. Le graphe G2 ayant une connexité moyenne plus faible que le graphe
G1, la ligne de transition T1 se situe à droite de T2. En conséquence, la zone B est plus petite pour le
graphe G2. Entre les deux lignes de transitions, il est alors possible de trouver des combinaisons du taux
d'activité des sites et du taux d'activité des liens, tel qu'un amas percolant apparaisse dans le graphe G1 et pas
dans le graphe G2 (Clerc et alii, 1983, p. 11).
Dans le plan (ps, pb), l'intersection de chaque ligne de transition avec les côtés du carré
unitaire met en évidence deux points particuliers. Pour le graphe G1, les coordonnées de ces
points sont (pcs(G1), 1) et (1, pcb(G1)). Les valeurs pcs(G1) et
pcb(G1) sont respectivement le seuil de percolation de sites et le seuil de percolation de
liens du graphe G1. De même pour G2, la ligne de transition T2 coupe le carré unitaire aux
coordonnées (pcs(G2), 1) et (1, pcb(G2)), où pcs(G2) et
pcb(G2) correspondent respectivement au seuil de percolation de sites et de liens du
graphe G2.
La détermination de la courbe critique T pour chaque graphe G de taille infinie est impossible
car particulièrement complexe (Hammersley et Welsh, 1980, p. 596)13. Une
caractéristique de la probabilité de percolation universellement vérifiée à travers les graphes,
peut malgré tout être soulignée : la percolation est plus facile à travers les liens qu'à travers
les sites. Notée de façon formelle, cette propriété se traduit par : P(p, 1) £ P(1,
p) " 0 £ p £ 1
Ce résultat, déjà suggéré en étudiant la
figure 1.26, se généralise de la façon suivante (Hammersley, 1980, repris dans
Hammersley et Welsh, 1980, pp. 596-597) : P(d ps, pb) £ P(ps, d
pb) " 0 £ ps £ 1, 0 £ pb £ 1, 0
£ d £ 1
Ceci conduit à deux autres inégalités. La première reprend l'idée
d'une probabilité de percolation plus importante dans des combinaisons (ps, pb) symétriques,
lorsque la probabilité d'activité des sites est favorisée : P(p1, p2) £ P(p2,
p1) " 0 £ p1 £ p2 £ 1
La seconde hiérarchise les
probabilités de percolation selon diverses combinaisons des taux
d'activité. Une baisse du taux d'activité des liens en contre partie
d'une augmentation du taux d'activité des sites est toujours supérieure ou équivalente à la
situation initiale pour obtenir un amas percolant : P(p1 p2 , 1) £ P(p1 , p2)
£ P(1, p1 p2) " 0 £ p1 £ 1, 0 £ p2
£ 1
En conséquence, pour lutter contre la propagation d'une maladie (voir
§ 1.2.3, p. ??), il apparaît plus efficace d'agir sur la susceptibilité
(ps) de la population que sur la virulence du microbe, c'est-à-dire les risques d'infection
entre les membres (pb) (Hammersley et Welsh, 1980, p. 597).
Lors de la définition du seuil de percolation, une ambiguïté est née sur le degré de certitude lié
à la présence d'un amas percolant sur le réseau. Selon la théorie, au dessus du seuil critique un
amas infini apparaît de façon certaine dans un réseau de taille infinie. De façon empirique on
précise seulement qu'il existe une probabilité positive de percolation. Cette différence tient à
l'effet dit de « taille finie » du réseau.
1.3.2 L'effet de taille finie
Dans des systèmes finis comme ceux simulés sur un ordinateur, la valeur déterminée n'est
généralement pas la valeur exacte du seuil. Ainsi, chaque valeur obtenue par des méthodes
numériques ou expérimentales doit être extrapolée avec précaution à un système de taille infinie
(Stauffer et Aharony, 1992, p. 17). Après une présentation de la problématique liant la limite
thermodynamique à la taille des réseaux, les propriétés des frontières puis la distinction entre la
probabilité individuelle et le taux global seront exposés. Enfin, les notions de longueur de
corrélation et de lois d'échelle seront abordées.
Limite thermodynamique et taille du réseau
Les régimes spatiaux s'associent à la notion de limite thermodynamique, ce qui peut être
mis en parallèle avec le régime asymptotique des problèmes temporels plus courants en
économie.
La limite thermodynamique d'un système situé dans un espace de dimension d s'obtient sous deux conditions (Lesne,
1996, p. 18). D'une part, la taille linéaire du système L doit être considérée comme infinie à l'échelle des
constituants élémentaires, ce qui en parallèle permet l'analyse de leur corrélation statistique14. D'autre part,
les effets de bords doivent pouvoir être négligés. Ceci autorise alors une invariance par translation, le placement
arbitraire de l'origine spatiale et l'élimination des caractères non universels liés à la forme du système. Après le
calcul des grandeurs globales, il faut dans un premier temps diviser ces grandeurs par Ld pour les ramener à des
grandeurs volumiques. Dans un second temps, on détermine la limite thermodynamique en faisant tendre L vers l'infini
pour une même densité.
Le régime asymptotique est l'équivalent temporel de la limite thermodynamique (Lesne, 1996, p. 19).
Il s'associe sur un intervalle de temps [t0 , t0 + T] à une évolution observée sous deux
conditions. Premièrement, t0 doit être relativement important pour qu'un régime permanent puisse
s'instaurer, s'il existe. En conséquence, les conditions initiales (analogues temporels des
conditions aux bords) peuvent être évincées. Deuxièmement, T doit être grand afin que l'ensemble
des caractéristiques de court, moyen et long terme soit observé. Autrement dit, T (analogue
temporel de L), doit être de taille macroscopique pour que la divergence d'un temps
caractéristique t soit réelle sous la contrainte t < T.
La modification des caractéristiques critiques provenant du fait que la limite thermodynamique
n'est pas atteinte est appelée « effet de taille finie ». La question est alors de savoir comment
varient les résultats dans un réseau de taille importante mais limitée. Si la taille du réseau est
finie, il existe une probabilité non nulle d'obtenir un amas reliant les bords opposés du réseau,
quelle que soit le taux d'activité (Stauffer et Aharony, 1992, pp. 71-72). Soit P (p, L) la
probabilité qu'un réseau de dimension linéaire L percole avec un taux d'activité p. Dans un
système infini, P = 0 lorsque p est inférieur à pc et P = 1 pour p supérieur à
pc. De cette façon, la dérivée de P sur p indique la probabilité que le réseau commence à
percoler si le taux d'activité augmente de p à p + dp. La
figure 1.28 montre l'évolution schématique de P et d P /
d p dans un réseau de taille finie et dans un réseau de taille infinie.
Figure 1.28: Probabilité de percolation et taille du réseau
 |
| Source : Stauffer et Aharony (1992), p. 72 |
Cette évolution schématique de P (p, L) est confirmée par l'étude expérimentale de la
probabilité de percolation obtenue par simulation, pour différentes tailles d'échantillons (Clerc
et alii, 1983, p. 28). Dans le contexte d'un réseau électrique, on parle de probabilité de
conduction. Celle-ci notée Fn(p), est équivalente à la probabilité de percolation P (p,
L), puisque la percolation et la conduction sont définies de façon identique : présence d'un amas
reliant les bords opposés. Les résultats expérimentaux dans un réseau carré de sites pour
des échantillons de taille N = n2 éléments sont représentés sur la
figure 1.2915.
Figure 1.29: Probabilité de conduction et taille du réseau
 |
| Source : Clerc et alii (1983), p. 28 |
Pour une taille n donnée, l'évolution de Fn(p) suit la forme d'une courbe logistique. Ainsi,
la probabilité de conduction reste minime pour de faibles valeurs de p alors que pour des valeurs
élevées la probabilité est quasi-unitaire. Lorsque la taille de l'échantillon augmente, la pente de
la probabilité de conduction s'élève et à la limite, tend vers l'infini à la verticale du seuil de
percolation. Une zone de transition où la probabilité de conduction est comprise entre 10 et 90 %,
est définie par les valeurs p1 et p2 telle que : Fn(p1) = 0,1 et Fn(p2) = 0,9. Pour
l'échantillon de taille n = 20, la mesure des valeurs de p1 et p2 a été précisée sur la
figure 1.29. Ces valeurs sont transcrites sur la figure 1.30
qui confirme l'idée que la zone de transition est d'autant plus faible que la taille du réseau est
grande (Clerc et alii, 1983, p. 29).
Figure 1.30: Zone de transition et taille du réseau
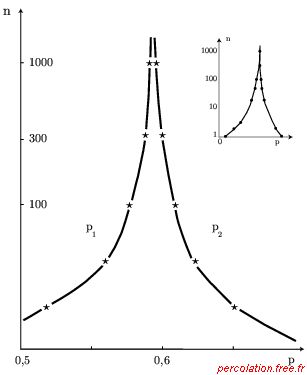 |
| Source : Clerc et alii (1983), p. 29 |
La courbe complète de p = 0 à 1 pour n = 1 à 1 000, dans un réseau carré, est reprise en médaillon de la
figure 1.30. L'effet de taille finie apparaît ainsi de moins en moins important lorsque la taille du
réseau est grande. Dans les simulations effectuées pour n = 1 000, la valeur du seuil de percolation estimée est pc =
0,59 ± 0,01.
Les frontières du système
L'existence et la nature des frontières ont une influence sur la connexité du système dans son
voisinage, à travers les effets de bords dans les simulations numériques ou les
effets de surfaces dans les simulations analogiques (Clerc et alii, 1983, p. 92).
Dans ces conditions, cette variation locale peut avoir des conséquences sur l'ensemble du système
par le biais d'un effet double :
-
un site à la frontière ayant moins de voisins que ceux au milieu du réseau, la probabilité
qu'il soit connecté à l'amas infini est plus faible (effet de « déplétion ») ;
- selon le problème considéré, la probabilité de distribution des liens peut
prendre une valeur différente à la frontière et à l'intérieur.
Dans un réseau de taille L en dimension d, un raisonnement qualitatif montre que le nombre
d N d'éléments touchés par les effets de bords va varier comme Ld – 1, sauf pour des
géométries très spéciales (Lesne, 1996, p. 19). À densité constante, le nombre total N d'éléments
varie comme Ld. Dans la limite thermodynamique L ® ¥, la proportion d N /
N tend alors vers 1 / L, c'est-à-dire zéro. Il devient ainsi possible de négliger les effets de
bords.
Pour limiter les effets de taille finie des échantillons, il existe diverses méthodes agissant
notamment sur les frontières du réseau (Gaylord et Nishidate, 1996, pp. 7-8) :
-
La solution la plus fréquemment employée consiste à poser des frontières
périodiques, c'est-à-dire des conditions aux limites périodiques16. Dans le cas d'un réseau carré, le réseau se replie sur lui-même
pour former un tore17. Les sites de la première ligne sont alors voisins de ceux de la dernière ligne, et la
première colonne se trouve jointe à la dernière. L'ensemble des sites à l'intérieur ou sur les bords du réseau ont
alors le même nombre de voisins.
- Une autre méthode assigne une propriété définitive aux sites placés à la frontière. Il
peut s'agir de frontières absorbantes (ouvertes) ou de frontières réfléchissantes
(fermées) selon que respectivement elles effacent où redistribuent l'« information » provenant de
l'intérieur du réseau.
- La possibilité de frontières mobiles est une autre solution. Dans l'étude
dynamique d'un problème de percolation par exemple, la taille du réseau augmente alors à chaque
itération. Les effets de bords peuvent ainsi être négligés.
- Enfin la
dernière solution contourne le problème en choisissant pour point de départ un site actif et non un
réseau de taille fixée ex-ante. Dans ce cas, les propriétés de l'amas s'analysent en
associant à ce site « instigateur » des sites voisins de plus en plus nombreux (Clerc et
alii, 1983, p. 26).
Probabilité individuelle versus taux global
Un autre problème lié à la taille finie des réseaux simulés touche la définition de p. Dans un
système d'extension infinie, il est statistiquement équivalent de parler d'une probabilité
individuelle p que chaque site soit actif, ou d'un taux global d'activité de p sur l'ensemble
de la population. Pour un échantillon fini par contre, cette équivalence n'est plus totalement
assurée. Lorsque le réseau est de petite taille, il est probable que le nombre de sites d'un type
donné sera légèrement différent de p % de la population globale, si l'état de chaque site est
décidé individuellement.
De façon plus formelle, les configurations d'un échantillon de N sites sont décrites par [
e ] où ej = 1 si le site j Î
Zd est actif (probabilité p) et ej = 0 s'il
est inactif (Lesne, 1996, p. 316). Dans cette situation, le nombre de sites actifs N0 est une
variable aléatoire N0 (p, N, [e]) . Par conséquent, la concentration
correspondant au taux global, devient elle aussi une variable aléatoire c(p, N, [e])
= N0 (p, N, [e]) / N = åj ej
/ N. Il est alors possible de montrer que lorsque N tend vers l'infini, la concentration
aléatoire correspond à la probabilité p qu'un site soit occupé : Cette démonstration s'applique,
quel que soit le réseau, aussi bien aux modèles de percolation de sites qu'aux modèles de
percolation de liens.
Dans une simulation, il est par conséquent techniquement préférable de considérer que p % de la
population est d'un type donné, par exemple Z, puis de distribuer ces éléments de façon aléatoire
sur le réseau, plutôt que de tirer individuellement le type de chaque site avec une probabilité p
d'être Z (voir Pajot, 1996-b, p. 61 et p. 63).
Longueur de corrélation et lois d'échelle
La taille finie des réseaux apparaît comme un inconvénient dans la précision des calculs liés au
seuil de percolation et aux autres grandeurs statistiques. Lorsque p est inférieur au seuil
critique, le réseau est formé d'amas de toutes tailles allant de l'unité jusqu'à une longueur
maximale. Cette valeur maximale correspond à la longueur de corrélation du système (Guyon
et Roux, 1987, p. 1053). Dans un réseau de taille infinie, la longueur de corrélation devient
infinie au seuil de percolation. À l'approche du seuil, l'échelle de taille sur laquelle il
faudrait effectuer une moyenne devient par conséquent de plus en plus grande.
De façon générale, les phénomènes critiques spatiaux ne se manifestent que dans la limite
thermodynamique. Dès lors, la divergence d'une longueur de corrélation n'est observable que dans un
système d'extension L infinie. Au point critique q = q c, les caractéristiques du
système sont alors celles de grandeurs thermodynamiques, les quantités X(L, q) étant
régulières en q (Lesne, 1996, p. 82) :
L'influence de la taille finie L des réseaux simulés ou expérimentaux est imperceptible loin du
voisinage du ou des points critiques car les corrélations statistiques sont de courte portée : x
« L. Dans cette situation, le système SL est une juxtaposition de sous-systèmes
statistiquement indépendants de taille x, et qui sont individuellement représentatifs de
l'état macroscopique du système S (Lesne, 1996, pp. 82-83). Ainsi, les grandeurs
observées sur un réseau dont la taille est supérieure à x correspondent parfaitement aux
valeurs déterminées dans la limite thermodynamique. Au voisinage de la valeur critique q c,
la longueur x (q ) des corrélations augmente et devient de l'ordre de la taille du réseau.
Les fluctuations statistiques étant déterminantes, la nature stochastique des grandeurs XL
obtenues ne peut être négligée. De façon numérique ou expérimentale, l'information n'existe que sur
la réalisation des grandeurs, dont la distribution dépend de L, et qui par conséquent ne peut
plus être assimilée aux grandeurs déterministes X¥ du système d'extension infinie.
Pour décrire le comportement d'une grandeur globale X(L, q ) dans un système de taille
L au voisinage du point critique ( q ® q c ), les hypothèses suivantes
sont proposées (Lesne, 1996, pp. 83-84) :
-
dans la limite thermodynamique L ® ¥, on observe la loi
d'échelle :
X¥ (q) ~ (q – q c )– g (g > 0)
- pour L < ¥, X(L, q) est une fonction régulière de L et q ;
- au point critique q = q c, on suppose que X suit une loi d'échelle
X(L, q c) ~ La d'exposant a encore indéterminé (cette hypothèse est connue sous
le nom de finite size scaling hypothesis) ;
- le comportement critique possède une seule échelle caractéristique, la longueur x
(q ) ~ |q – q c |– n des corrélations statistiques.
De là, on recherche pour X une dépendance de la forme (Lesne, 1996, p. 84) : X(L, q)
~ LaF [L1/n (q – q c) ]
où F(z) a pour échelle caractéristique
D z = 1. En comparant limL ® ¥ XL (q ) et X¥ (q
) on déduit que F(z) se comporte comme |z|– g à l'infini et que a = g /
n. En taille finie, la loi d'échelle L = x (q) ~ |q – q c|– n
coïncide avec la loi d'échelle thermodynamique. Ainsi, pour une taille L supérieure à la longueur
de corrélation x (q), la loi d'échelle est valide. Dans le cadre de la percolation, un
réseau de taille finie peut, par conséquent, être considéré comme pratiquement infini ou non, pour
une valeur de p donnée, suivant que sa dimension linéaire L est grande ou non devant la
longueur de corrélation x (p).
Pour résumer, les incertitudes liées aux effets de taille limitent la précision des calculs mais
elles ont cependant un avantage : elles permettent d'analyser le comportement de la longueur de
corrélation (Clerc et alii, 1983, pp. 29-30). En effet, à l'approche de pc, la façon
dont x (p) tend vers l'infini en fonction de p se réalise selon une loi puissance. Cette loi
est de la forme |p – pc|– n où n est un exposant critique, c'est-à-dire qu'il
est indépendant de la géométrie du système au voisinage de pc (Guyon et Roux, 1987,
p. 1054)18.
Dans notre travail, sauf cas particulier, les réseaux seront posés (taille suffisante ou propriétés
spécifiques des frontières) de façon à pouvoir négliger les effets de taille finie. En conséquence,
la présence d'un amas percolant sera considérée certaine dès lors que le seuil critique pc est
franchi. De plus, le paramètre p sera supposé équivalent d'un point de vue individuel ou global.
Les termes de probabilité individuelle et de taux moyen sur la population seront par suite employés
indifféremment.
À plusieurs reprises dans ce chapitre, l'intérêt s'est porté sur le modèle de percolation carré de
sites où la valeur du seuil critique se situe aux alentours de pc ~ 0,59. Contrairement à
l'intuition qui amènerait à penser que pc = 1/2 par symétrie ou qu'il s'agit d'une variable
aléatoire, cette concentration a une valeur bien déterminée et différente de 1/2 dans un réseau
d'extension infinie (Lesne, 1996, p. 317).
1.3.3 Détermination du seuil
Les méthodes mathématiques qui permettent de calculer pc de façon exacte sont jusqu'à présent limitées à des
dimensions inférieures à trois. Dans bon nombre de situations, même simple, l'approximation est alors
nécessaire19. Après deux exemples de calculs exacts
du seuil de percolation, nous aborderons un premier type d'estimation par la détermination numérique, puis un deuxième
avec la méthode des séries et un troisième avec les méthodes de renormalisation. Enfin, les valeurs du seuil dans
différents réseaux seront présentées.
Solution exacte en dimension un
Le problème de percolation peut être résolu de façon exacte en dimension un (Stauffer et Aharony,
1992, pp. 19-20). Le réseau correspond à une chaîne linéaire où les sites sont occupés avec une
probabilité p. Les amas sont alors des groupes de sites actifs voisins. Un amas ne contient pas
de sites inactifs en son sein. S'il est de taille finie cependant, il est nécessairement bordé par
un site inactif à gauche et à droite (figure 1.31).
Figure 1.31: Exemple d'amas en dimension un
 |
| Source : Stauffer et Aharony (1992), p. 19 |
Soit p la probabilité d'activité d'un site sachant que cette activité est indépendante de celle des autres sites. La
probabilité que x sites soient occupés est alors px, les événements étant statistiquement indépendants. La
probabilité pour qu'un site soit inactif est (1 – p). Si p = 1, l'ensemble des sites sont occupés et la chaîne ne forme
qu'un amas unique. Quel que soit p inférieur à un, des « trous » viendront couper cet amas là où un site sera
inactif. Ainsi, une chaîne de taille L aura en moyenne (1 – p)L sites inactifs. Lorsque L tend vers l'infini, le
nombre moyen de sites inactifs tend également vers l'infini. L'existence d'un seul site inactif brise l'amas qui
connecte les deux extrémités. En d'autres termes, lorsque p est inférieur à un, il n'y a pas d'amas percolant. Par
conséquent, le seuil de percolation est pc = 1. Dans ce cadre d'analyse, il est impossible d'observer le
comportement du système pour des valeurs de p > pc.
Solution exacte dans le réseau de Bethe
Le réseau de Bethe représenté sur la figure 1.14 (p. ??), permet lui
aussi le calcul exact du seuil de percolation (Stauffer et Aharony, 1992, pp. 27-28). La structure
arborescente se définit par un même nombre z de plus proches voisins pour chaque site. Ainsi, il
existe z liens partant de l'origine. Chaque lien se termine par un autre site d'où partent
également z liens. Obtenir un amas percolant revient alors à partir de l'origine et à trouver un
chemin infini de sites actifs. En se dirigeant vers l'extérieur, il existe (z – 1) nouvelles
directions sur chaque nouveau site. Chacun de ces nouveaux liens conduit à un nouveau voisin qui
est actif avec une probabilité p. Par conséquent, il existe en moyenne (z – 1)p nouveaux sites
sur lesquels il est possible de continuer le chemin. Si ce nombre est inférieur à un, le nombre
moyen de chemins différents conduisant à l'infini décroît à chaque génération d'un facteur
inférieur à l'unité. Ainsi, même si tous les sites voisins sont actifs et même si z est grand,
lorsque p < 1 /(z – 1) la probabilité de trouver un chemin continu tend vers zéro de manière
exponentielle avec la longueur du trajet. Le seuil de percolation dans le réseau de Bethe est par
conséquent pc = 1 /(z – 1), avec z le nombre de voisins de chaque site.
La démonstration étant également possible en considérant que l'activité des liens est aléatoire, la
formule apparaît valide aussi bien pour la percolation de sites que la percolation de liens.
Détermination numérique
Une autre méthode d'estimation de pc est la détermination numérique. Celle-ci réside dans
l'observation de phénomènes de transports qui ne sont possibles que s'il existe un amas percolant
(par exemple, la conduction électrique sur la figure 1.16,
p. ??). L'analyse statistique des valeurs du seuil obtenues sur un nombre
important de configurations d'extension finie donne la limite déterministe de pc.
À titre d'illustration, la figure 1.32 reprend les résultats d'une simulation effectuée par la
méthode de Monte-Carlo dans un réseau carré de liens (Kirkpatrick, 1979, repris dans Binder et Heermann, 1997,
p. 41).
Figure 1.32: Détermination du seuil dans un réseau carré de liens à deux dimensions
 |
| Source : Kirkpatrick (1979), repris dans Binder et Heermann
(1997), p. 41 |
Les courbes représentent la proportion d'échantillons conducteurs pour une valeur de l'activité des
liens donnée p, dans des réseaux de tailles différentes. Un échantillon est dit conducteur, si un
amas percolant relie les bords du réseau. Le seuil de percolation pc est obtenu au point
d'intersection de ces différentes courbes.
L'étude d'un phénomène de transport peut se faire en utilisant diverses techniques, comme par
exemple (Lesne, 1996, pp. 318-318):
-
le modèle de contagion qui simule la propagation des feux de forêts où à une
valeur pc (n) déterministe, on observe la divergence du temps t (p, N) mis par le feu
pour aller du bord gauche au bord droit du réseau, p étant la probabilité pour un site d'être un
arbre sur le réseau de taille n × n (méthode de Monte-Carlo20) ;
- le modèle de diffusion21 sur un support lacunaire, où l'on
observe que le déplacement quadratique moyen D (t, p) d'une particule reste borné au
cours du temps pour 0 £ p < pc ou diffuse de façon asymptotiquement normale pour pc <
p £ 1 ;
- les méthodes statiques purement géométriques comme l'algorithme d'Hoshen-Kopelman
où par itération d'une procédure d'indexation on peut estimer la moyenne des seuils de percolation
observés (Hoshen et Kopelman, 1976)22.
La méthode des séries
Dans l'estimation du seuil de percolation par la méthode des séries, nous allons faire appel à des notions qui ne
seront totalement explicitées que dans le § 1.4.1. La méthode consiste à déterminer par comptage direct
sur de petits échantillons, la statistique des amas sur le réseau et à l'extrapoler au moyen de développements
mathématiques (Clerc et alii, 1983, p. 20).
Soit t le périmètre, c'est-à-dire le nombre de sites inactifs plus proches voisins qui forment la bordure de
l'amas sur le réseau et gst le nombre de configurations géométriques différentes d'un amas de s sites et de
périmètre t. Le nombre moyen d'amas de taille s est alors : À titre
d'exemple, dans un réseau carré de sites en deux dimensions, pour s = 1 on a n1 = p (1 – p)4, pour s = 2 on a n2 =
2 p2 (1 – p)6 et pour s = 3 on a n3 = 2 p3 (1 – p)8 + 4 p3 (1 – p)7. Ces nombres d'amas ainsi obtenus, on calcule
l'analogue de la susceptibilité magnétique pour la percolation, c'est-à-dire le second moment de la distribution de la
taille des amas : ås s2 ns. À partir des expressions exactes ci-dessus, et en utilisant le théorème du
binôme, on peut calculer les premiers termes du développement :
|
s2 ns = |
|
am pm =
p + 4p2 + ... |
Si plusieurs des coefficients de ce développement sont connus, il devient possible d'en tirer le
comportement asymptotique au voisinage de pc. La limite am + 1 / a fournit alors une
estimation de 1 / pc, pour m très grand (Clerc et alii, 1983, p. 21).
La méthode de renormalisation
Les méthodes de renormalisation sont un autre moyen pour estimer le seuil de percolation et les exposants critiques
(Clerc et alii, 1983, p. 21). La possibilité de renormalisation tient à la propriété de
self-similarité23. L'idée de base tient dans l'hypothèse qu'il existe une seule échelle pour caractériser
le problème : la longueur de corrélation x qui diverge à pc (voir § 1.3.2,
p. ??). En effet, si l'on s'intéresse aux amas de diamètre L, avec L beaucoup plus grand
que le pas du réseau, il faut distinguer les situations où L < x et L > x. Pour p = pc on a une longueur de
corrélation infinie (x = ¥) et toutes les longueurs finies (L par exemple) sont beaucoup plus petites que
x. Par suite, l'échelle d'observation du système au seuil de percolation n'a plus d'importance car le système
apparaît semblable, à de simples facteurs d'échelle près, quelle que soit l'échelle utilisée. Il est alors possible de
renormaliser le système en ne prenant plus comme élément de base les sites, mais des régions de taille
inférieure à x ayant un diamètre de k pas du réseau initial24. Cette opération
peut être réitérée avec le même facteur d'échelle k, sur le nouveau réseau formé par ces éléments composites, etc. À
p = pc, aucun changement significatif ne peut intervenir à cause de cette renormalisation même après de nombreuses «
moyennes » de ce type. En ce sens, pc est un point fixe mathématique de la transformation de renormalisation.
L'étude des supersites ainsi créés, permet de déterminer la valeur du point critique qui correspond au seuil de
percolation25.
Pour le réseau triangulaire de sites par exemple, il est possible de déterminer la valeur du seuil
de percolation par renormalisation (Clerc et alii, 1983, pp. 22-23). L'ensemble des sites
du réseau peuvent se rassembler dans des triangles de trois éléments du réseau de base initial, tel
que chaque site n'appartienne qu'à un seul triangle26. Un supersite est placé au centre de chaque triangle et
représente la moyenne (au sens de la renormalisation) des sites qu'il renormalise. Le nouveau
réseau des supersites forme alors à son tour un réseau triangulaire, qui peut à son tour être
renormalisé dans un réseau de super-supersites (figure 1.33).
Figure 1.33: Renormalisation dans un réseau triangulaire de sites
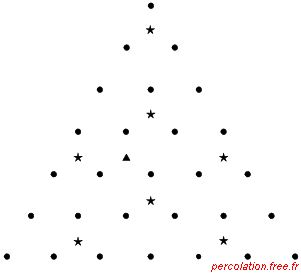 |
· : site ;  : « supersite » ; : « supersite » ;
 : « super-supersite » : « super-supersite » |
| Source : Clerc et alii (1983), p. 22 |
Dans chaque cas, le pas du nouveau réseau correspond au pas du précédent multiplié par un facteur
k = 31/2.
L'état (actif/inactif) d'un supersite est déterminé en fonction de l'état des sites du réseau initial qu'il
renormalise. Un supersite est considéré actif si au moins deux (la majorité) des sites qu'il renormalise sont actifs,
sinon il est inactif. Le tableau 1.4 montre qu'il existe trois configurations possibles
lorsque deux sites sont actifs (p2 (1 – p)), alors que par définition, il n'existe qu'une seule façon de répartir
trois sites actifs sur trois emplacements (p3).
Au total, la probabilité p' d'activité d'un supersite est : p' = p3 + 3 p2 (1 – p)
Au seuil
de percolation, les deux réseaux sont identiques, ce qui se traduit par : p = p' = pc
La
solution non triviale (pc ¹ 0, pc ¹ 1) du système formé par les deux équations est
pc = 1/2. Par conséquent, le seuil de percolation dans un réseau triangulaire de sites est pc
= 1/2.
Valeurs du seuil de percolation
Le seuil de percolation pc dépend du modèle de percolation choisi, de la géométrie ainsi que de
la dimension d du réseau et non de l'interprétation physique des sites occupés ou des liens
présents, ni de la façon dont on réalise l'augmentation de p à partir de zéro (Lesne, 1996,
p. 317). Ceci est une des caractéristiques fondamentales de l'aspect universel de la
percolation. Le tableau 1.5 indique les valeurs exactes (*) ou
approchées des seuils de percolation selon la forme du réseau, sa dimension et le modèle de
percolation (pcb : percolation de liens ; pcs : percolation de sites).
Table 1.5: Valeurs du seuil de percolation
| |
Réseau |
pcb : LIENS |
pcs : SITES |
z |
| 2D |
Nid d'abeille (hexagonal) |
1 – 2 sin(p /18) * |
0,697 |
3 |
Kagomé |
0,525 |
1 – 2 sin(p /18) * |
4 |
Carré |
1/2 * |
0,593 |
4 |
Triangulaire |
2 sin(p /18) * |
1/2 * |
6 |
| 3D |
Diamant |
0,388 |
0,430 |
4 |
Cubique simple |
0,247 |
0,307 |
6 |
Cubique centré |
0,178 |
0,243 |
8 |
Cubique faces centrées |
0,119 |
0,195 |
12 |
Hexagonal |
0,124 |
0,204 |
12 |
| (*) : valeurs exactes |
| Source : Clerc et alii (1983), p. 12 |
Il précise également la coordinence z, c'est-à-dire le nombre de plus proches voisins d'un site
donné, pour différents réseaux. Les chiffres de ce tableau peuvent parfois légèrement différer des
valeurs annoncées dans d'autres travaux27. Ceci s'explique par la plus ou moins
grande qualité des simulations ainsi que de la précision des estimations.
Dans les systèmes étudiés jusqu'à présent, l'apparition d'un amas infini déterminait le seuil de
percolation. Si le problème est envisagé de façon inverse en partant d'un seuil, on peut préciser
le comportement du système face à la question du nombre d'amas percolant simultanément
envisageables.
1.3.4 Amas infini et seuil de percolation
Le problème de l'« unicité de l'amas infini » peut se considérer de deux façons. La première pose
la question du nombre d'amas possible pour une population donnée, et la seconde envisage la même
question mais sur les deux populations.
Unicité de l'amas infini d'une population
Dans un modèle de percolation, deux types d'éléments se trouvent répartis de façon aléatoire sur le
réseau. Dans le problème du mélange des billes conductrices en proportion p et isolantes en
proportion (1 – p), l'intérêt porte sur la population conductrice. Autrement dit, la théorie de la
percolation montre qu'à partir d'un pourcentage critique pc de billes conductrices, le système
devient conducteur et autorise le passage d'un courant électrique28. La
question de l'unicité de l'amas infini pour la population des billes conductrices
interroge alors sur le nombre d'amas percolants conducteurs qui peuvent s'envisager « en parallèle
» dans le réseau.
Pour répondre à cette question A.L. EFRÖS et B.I. SHKLOVSKII raisonnent en considérant
le mélange d'éléments noirs en proportion p et blanc en proportion (1 – p) (Efrös et Shklovskii,
1976, repris dans Clerc et alii, 1983, p. 20). Soit p1 une concentration voisine de
pc, on suppose que pour p tel que pc < p < p1, il existe deux amas infinis noirs
remplissant tout l'espace. Soit D < p1 – pc, alors pour une proportion p = pc + D /
2, les deux amas ont une densité finie et sont séparés par une distance finie. En
remplaçant des éléments blancs par des noirs, avec l'augmentation de p jusqu'à pc + D, le
nombre de liaisons possibles entre les deux amas devient infini. Chaque liaison a une probabilité
faible mais non nulle d'exister. Les deux amas sont alors joints, ce qui est contraire à
l'hypothèse de départ.
Plus formellement, dans un problème standard de percolation sur Zd, pour toute valeur de p,
soit il n'existe pas d'amas infini, soit il existe un seul amas infini (Aizenman et alii, 1987,
p. 15)29. Ainsi, il ne
peut coexister plusieurs amas percolants d'une même population dans un réseau. Par conséquent dans le mélange de billes
conductrices et isolantes, s'il existe un amas infini conducteur, il est unique.
Unicité de l'amas infini sur les deux populations
Le problème de l'unicité de l'amas infini se pose aussi lorsque l'intérêt porte sur les deux
populations en même temps. Dans ce cas, la présence d'un amas percolant pour une population
interdit-elle l'existence d'un amas percolant pour l'autre population ? En d'autres termes, est-il
possible que les deux populations puissent percoler en même temps ?
Intuitivement la réponse pourrait sembler triviale. En deux dimensions sur un réseau carré de
sites, si l'on place de façon aléatoire une proportion p de sites de type A et une proportion
(1 – p) de sites de types B, alors l'une ou l'autre des populations percole mais il est
impossible que les deux puissent le faire simultanément. En effet, d'un point de vue topologique,
l'amas infini de l'une des populations doit pouvoir aller dans toutes les directions ce qui empêche
l'autre population de percoler (Clerc et alii, 1983, p. 20). Dans un réseau infini de ce
type, la probabilité que les deux populations percolent simultanément est alors nulle. Cependant,
ce raisonnement n'est plus valable à trois dimensions. La coexistence d'amas infinis de types
différents peut s'envisager.
Les configurations possibles de la population dépendent des valeurs de p et pc dans le
système30. En fait, il existe des combinaisons de ces
deux paramètres pour que : soit aucune, soit les deux, soit l'une des populations percole (Corcos,
1993, pp. 272-275).
-
Pour qu'aucune des populations de type A ou B ne percole, il suffit que leurs
proportions respectives p et q = (1 – p) soient simultanément inférieures au seuil de percolation
pc. Ceci se traduit par :
ì
í
î |
|
Û |
ì
í
î |
|
Û |
ì
í
î |
|
Û 1 – pc < p < pc |
- Pour que les deux populations percolent, il faut que chacune des proportions p et q
soit supérieure au seuil de percolation pc. De là, on obtient le raisonnement suivant :
ì
í
î |
|
Û |
ì
í
î |
|
Û |
ì
í
î |
|
Û pc < p < 1 – pc |
- Enfin, pour que seulement l'une des populations percole,
il suffit quelle que soit p, que le seuil de percolation pc soit égal à 0,5 comme c'est le cas
dans le réseau carré de liens à deux dimensions.
Les différentes configurations sont résumées dans le tableau 1.6.
Table 1.6: Configurations percolantes des populations
| Seuil pc |
Proportion p de la population de type A |
Population(s) percolante(s) |
| [0 ; 0,5] |
[0 ; pc [ |
type B |
[ pc ; 1 – pc ] |
types A et B |
] 1 – pc ; 1] |
type A |
| ]0,5 ; 1 ] |
[0 ; 1 – pc ] |
type B |
] 1 – pc ; pc [ |
aucune |
[ pc ; 1 ] |
type A |
| Source : Corcos (1993), p. 274 |
Il montre l'importance de la structure du réseau (déterminant le seuil de percolation pc) et de
la proportion p correspondant au partage des deux types de populations du système.
Dans cette section consacrée à la notion de seuil de percolation, le caractère critique de cette
valeur a pu être mis en avant à travers les modèles de sites et de liens. De façon équivalente dans
le modèle mixte, la notion de ligne de transition a été décrite comme une combinaison des
proportions de sites et de liens actives dans le système. Une différence est alors apparue entre
les valeurs théoriques et les valeurs expérimentales. Ces problèmes liés à l'effet de taille finie
ont alors été présentés par le biais notamment des concepts de longueurs de corrélation et de lois
d'échelle. Par suite, diverses méthodes pour déterminer le seuil de percolation ont été décrites,
avant que les valeurs obtenues pour différents réseaux réguliers ne soient exposées. La relation
entre le seuil de percolation et les configurations percolantes des éléments du systèmes ont enfin
été développées avec la question de l'unicité de l'amas infini. Ainsi, le seuil de percolation se
révèle crucial en théorie de la percolation car il sépare les phases possibles du système. La
recherche de la valeur du seuil n'est cependant plus l'intérêt majeur du problème de percolation.
Le comportement de certaines grandeurs au voisinage du seuil semble plus riche en informations car
il montre des aspects plus universels.




















