1.4 Caractéristiques statiques
En considérant la percolation d'un point de vue statique, nous présenterons dans un premier temps les diverses
grandeurs qui la caractérise (§ 1.4.1). Pour rendre compte du comportement de ces grandeurs au
voisinage du seuil de percolation, ces statistiques conduiront dans un deuxième temps à la présentation des concepts de
lois d'échelle et d'exposants critiques (§ 1.4.2). Enfin, après une introduction au concept de
géométrie fractale, de nouvelles propriétés concernant les amas de percolation seront présentées
(§ 1.4.3).
1.4.1 Grandeurs caractéristiques
Dans un contexte statique, la situation d'un problème de percolation se décrit à travers quelques
grandeurs fondamentales comme le nombre d'amas de taille s normalisé par site, la probabilité
d'appartenir à l'amas infini, la taille moyenne des amas finis et les longueurs caractéristiques.
Nombre d'amas de taille s normalisé par site
La plus simple des grandeurs caractéristiques du problème de percolation est le nombre ns d'amas
de taille s, normalisé par site. Dans un échantillon fini comportant N sites, ns est la
moyenne du nombre d'amas de taille s : (1)31. Pour le réseau infini, ns est la limite de cette
moyenne lorsque le nombre de sites tend vers l'infini : (2) (Clerc et
alii, 1983, p. 16).
Pour un échantillon fini de N sites :
|
ns = |
| nombre total d'amas de taille s |
|
| N |
|
(1) |
Pour un réseau de taille infinie :
|
ns = |
|
|
| nombre total d'amas de taille s |
|
| N |
|
(2) |
En dimension un, le calcul de ns est trivial car le réseau correspond à une droite où la structure des sites est
régulière (figure 1.31, p. ??). Puisque l'activité des sites est aléatoire et
statistiquement indépendante, la probabilité pour que deux sites soient actifs est p2, pour trois p3, pour s
sites ps, etc32. Pour
obtenir un amas de taille s, il faut s sites actifs et deux sites inactifs (un de chaque côté). De manière
probabiliste ceci se traduit par ps (1 – p)2. La taille du réseau est N sites. Pour chaque site, la probabilité de
faire partie d'un amas de taille s étant ps (1 – p)2, le nombre d'amas de taille s est alors N ps (1 – p)2. Le
nombre ns étant une moyenne (voir (2)), pour la dimension d = 1 l'équation devient :
Cette définition (3) n'est cependant plus valide lorsque la dimension est supérieure
à un. En dimension deux dans un réseau carré par exemple, un amas de taille s peut avoir de
nombreuses configurations appelées « animaux »33. Selon la forme de l'animal, l'amas de taille s possède ainsi le même nombre de sites
occupés mais pas toujours le même nombre de sites inactifs. Prenons l'exemple de s = 4 et des
dix-neuf animaux qui y sont associés (figure 1.34).
Le chiffre situé sous chaque animal correspond au nombre de fois où l'on trouve cette
configuration. Pour la première configuration, il est possible de trouver quatre sites alignés de
façon verticale comme sur la figure 1.34, mais à une rotation près il est aussi
possible de les trouver horizontalement. Il existe alors deux possibilités pour obtenir cette
configuration sur le réseau carré. Ce chiffre correspond à la pondération qui s'associe à chaque
structure « site actifs / périmètre » pour le calcul de ns. À titre d'illustration, le
tableau 1.7 reprend les résultats du nombre d'animaux de taille s dans le
réseau carré, calculés par D.H. REDELMEIER34.
Table 1.7: Nombre d'animaux dans un réseau carré selon la taille de l'amas
| taille |
nombre |
taille |
nombre |
taille |
nombre |
| 1 |
1 |
9 |
9 910 |
17 |
400 795 844 |
| 2 |
2 |
10 |
39 446 |
18 |
1 540 820 542 |
| 3 |
6 |
11 |
135 268 |
19 |
5 940 738 676 |
| 4 |
19 |
12 |
505 861 |
20 |
22 964 779 660 |
| 5 |
63 |
13 |
1 903 890 |
21 |
88 983 512 783 |
| 6 |
216 |
14 |
7 204 874 |
22 |
345 532 572 678 |
| 7 |
760 |
15 |
27 394 666 |
23 |
1 344 372 335 524 |
| 8 |
2 725 |
16 |
104 592 937 |
24 |
5 239 988 770 268 |
| Source : Redelmeier (1981), (voir note de bas de page n° 1.4.1, p. ??) |
Le périmètre (noté t) est défini comme le nombre de voisins inactifs de l'amas qui sont notés
«×» sur la figure 1.34. Il tient compte des sites autour de l'amas mais aussi de ceux qui se
trouvent à l'intérieur d'éventuels trous. En dimension un, t = 2 quelle que soit la taille de l'amas alors que dans des
dimensions supérieures, il existe de multiples valeurs de t pour une même taille d'amas. Dès lors, il n'est plus
possible de fixer l'exposant de (1 – p) à deux pour le calcul de ns. On note gst le nombre de configurations
d'amas de taille s et de périmètre t. Le calcul du nombre d'amas de taille s normalisé par site devient alors
(Stauffer et Aharony, 1992, p. 25) :
La probabilité pour qu'un site arbitraire soit actif et élément d'un amas de taille s est par conséquent s ns,
c'est-à-dire le nombre de sites dans un amas multiplié par le nombre de ces amas normalisé par site. Si, par exemple,
sur un échantillon de taille N = 100, on observe neuf amas de taille s = 2, la probabilité qu'un site soit actif et
dans un amas de taille deux est : 2 × (9/100) = 0,18. Cette probabilité correspond alors exactement à la
fréquence observée du nombre de sites dans des amas de taille deux : 18 %.
Le nombre total d'amas de toute taille, noté G(p), normalisé par site est (Clerc et
alii, 1983, p. 14) :
Probabilité d'appartenir à l'amas infini
Soit P¥ (p) la probabilité qu'un site appartienne à l'amas infini. Dans un échantillon de
taille finie, la probabilité qu'un site soit un élément de l'amas percolant se détermine en faisant
le rapport du nombre de sites dans l'amas infini par le nombre total de sites actifs :
|
P¥ (p) = |
| nombre de sites de l'amas infini |
|
| nombre de sites actifs |
|
(6) |
Lorsque p < pc, il n'existe pas d'amas infini. Par conséquent, la probabilité d'y être attaché est nulle. À p =
pc, le caractère lacunaire de l'amas infini suggère qu'il occupe une fraction nulle du réseau (Lesne, 1996, p. 320).
Enfin, si p > pc, les simulations et les expériences amènent à supposer un comportement critique. De façon
formalisée, ceci se résume par :
|
|
ì
í
î |
| P¥ (p) = 0 |
si |
p £ pc |
| P¥ (p) » (p – pc) b |
si |
p ³ pc |
|
|
(7) |
En dimension d £ ¥, l'observation expérimentale de la probabilité d'appartenir à l'amas infini en
fonction de p montre la divergence de la dérivée [ d P¥ / d p ](p) au seuil de percolation, car le graphe
de P¥ (p) possède une tangente verticale en pc (Lesne, 1996, p. 320). Ceci illustre le caractère critique
de la transition à p = pc. La relation décrite pour p ³ pc est appelée « loi d'échelle » et l'exposant
b qui en est issu est qualifié d'« exposant critique ». Ces deux notions feront l'objet du paragraphe suivant
(voir § 1.4.2).
Selon la même logique que pour l'amas infini, il est possible de calculer la probabilité
d'appartenir à un amas fini. Dans un échantillon, cela revient à rapporter le nombre de sites
actifs en amas fini au nombre total de sites :
|
|
|
s ns = |
| nombre de sites en amas fini |
|
| nombre total de sites
actifs ou non |
|
(8) |
Sachant P¥ (p), la probabilité qu'un site ne soit pas élément de l'amas infini est
1 – P¥ (p). Pour qu'un site appartienne à un amas fini, il faut qu'il soit actif. En
conséquence, la probabilité pour qu'un site fasse partie d'un amas fini est :
|
|
|
s ns = p (1 – P¥ (p))
(9) |
Pour p < pc, il n'existe pas d'amas infini d'où P¥ (p) = 0. Dans (9), la
probabilité qu'un site arbitraire appartienne à un amas fini est alors égale à la probabilité p
qu'il soit occupé.
Taille moyenne des amas finis
La probabilité qu'un site quelconque appartienne à un amas de taille s est ns s, et celle
qu'il fasse partie de n'importe quel amas fini est ås s ns. Soit ws la probabilité que
l'amas auquel appartient un site actif arbitraire contienne exactement s sites :
De là, la taille moyenne des amas finis se calcule telle que :
Cette définition du nombre moyen de sites par amas fini reste valable à la condition que l'amas
infini, s'il existe, soit exclu de la somme. En intégrant (9), le calcul de la taille
moyenne des amas finis devient :
|
S(p) =
|
ì
ï
ï
í
ï
ï
î |
|
|
(12) |
Longueurs caractéristiques
La fonction de corrélation Cfini (p, r) se définit comme la probabilité qu'un
site r0 + r (à une distance r d'un site r0) soit
occupé et fasse partie du même amas que r0, sachant que celui-ci est actif et qu'il
n'appartient pas à l'amas infini (Lesne, 1996, p. 322). Cette grandeur est normalisée telle que
Cfini (p, r) = 1 pour une distance r = 0. La fonction de corrélation
pour l'amas infini Cinfini (p, r) suit la même définition pour des valeurs de p
> pc. À chacune de ces fonction de corrélation sont associées des longueurs
caractéristiques selon les définitions suivantes :
|
xfini2 (p) = |
|
r2 Cfini (p, r) ·
|
é
ê
ê
ë |
|
Cfini (p, r) |
ù
ú
ú
û |
|
(13) |
|
xinfini2 (p) = |
|
r2 Cinfini (p, r)
· |
é
ê
ê
ë |
|
Cinfini (p, r) |
ù
ú
ú
û |
|
(14) |
Les longueurs de corrélation xfini (p) pour 0 £ p £ 1 et
xinfini (p) pour pc £ p £ 1, sont un premier type de longueur
caractéristique. Celles-ci sont non nulles alors que l'état de chaque site est indépendant de
l'état des autres sites. Le rayon de giration moyen xg (p) des amas finis est une
deuxième façon de préciser la longueur caractéristique. Il s'interprète comme une longueur de
connexité. La troisième catégorie de longueur caractéristique est l'échelle x¥
(p) au dessus de laquelle l'amas infini est homogène.
Pour terminer sur les grandeurs caractéristiques d'un problème de percolation, la
figure 1.35 représente le schéma d'évolution et de dépendance de quelques
grandeurs en fonction de la proportion de sites actifs p.
Figure 1.35: Évolution et dépendance de quelques grandeurs en fonction de p
 |
| Source : Sahimi (1994), p. 13 |
Le modèle de percolation correspond ici à un modèle de sites dans un
réseau cubique simple. La probabilité d'appartenir à l'amas infini est notée P¥ (p). La
proportion de sites actifs qui font partie de l'amas infini est notée XA (p). La proportion de
sites actifs et isolés est représentée par XI (p). Enfin, la proportion de sites dans
l'épine dorsale (Backbone) est notée XB (p). Cette dernière grandeur
correspond aux sites actifs appartenant à l'amas infini débarrassé de ses bras morts
35. En référence avec l'électricité, cette épine dorsale est formée
par les éléments à travers lesquels passe le courant : les boucles et les liens
sensibles36. L'épine dorsale d'un amas percolant a un rôle
fondamental, car selon le degré de complexité des chemins conducteurs, elle influence les
propriétés de transport dans le système (Sahimi, 1994, p. 12).
1.4.2 Lois d'échelle et exposants critiques
La valeur des grandeurs obtenues dans un problème de percolation dépend des éléments microscopiques
du système comme par exemple la coordinence. Cependant, au voisinage du seuil critique, la plupart
de ces grandeurs ont des comportements qui sont indépendants de la structure du réseau et des
détails microscopiques (Sahimi, 1994, p. 14). Après un exposé des diverses lois d'échelle qui
décrivent ces comportements en théorie de la percolation, elles seront mises en évidence dans le
cas du réseau de Bethe. Chaque exposant critique étant lié à une loi d'échelle particulière, nous
évoquerons enfin les relations qu'entretiennent les divers exposants ainsi que les estimations de
leurs valeurs respectives.
Lois d'échelle
Au voisinage de pc, l'insensibilité du comportement des grandeurs caractéristiques d'un problème
de percolation aux détails microscopiques de la structure sur lequel il évolue, se résume dans les
relations appelées « lois d'échelle ». Celles-ci concernent principalement x (p), P¥
(p), S(p) et ns (p). Le degré de validité de ces relations n'étant pas totalement connu, les
termes des diverses équations seront séparés par la relation logarithmique »37.
Pour des valeurs inférieures au seuil aussi bien que pour des valeurs supérieures, la taille
linéaire des amas finis se caractérise par la longueur de corrélation x. Elle se définit comme
la distance moyenne entre deux sites du même amas. Au voisinage de pc, c'est-à-dire lorsque p –
pc est faible, la longueur de corrélation augmente selon (Bunde et Havlin, 1991, p. 56) :
|
|
| x(p) » |p – pc|– n |
pour |
p ® pc |
|
(15) |
Pour un site, la probabilité d'appartenir à l'amas infini P¥ (p) dépend de la proportion
d'éléments actifs. Au voisinage du seuil critique, la décroissance de P¥ (p) vers 0
s'effectue selon une loi puissance de p – pc au fur et à mesure que p tend vers pc par
valeurs supérieures. De façon formelle, ceci se traduit par (Grimmett, 1989, p. 149) :
|
|
| P¥ (p) » (p – pc) b |
pour |
p ¯ pc |
|
(7) |
La taille moyenne des amas finis S (p) suit également une loi d'échelle. Au voisinage de pc, son évolution est
supposée diverger selon la relation suivante (Bunde et Havlin, 1991, p. 56) :
|
|
| S(p) » |p – pc|– g |
pour |
p ® pc |
|
(16) |
À p = pc, le nombre d'amas de taille s normalisé par site est supposé différentiable deux fois
mais pas trois. On postule alors que la troisième dérivée de ns satisfait la relation (Grimmett,
1989, p. 150):
|
|
| n'''s » |p – pc|– 1 – a |
pour |
p ® pc |
|
(17) |
Les lois d'échelles insistent sur le caractère critique de la transition de percolation. Elles
rendent compte de l'évolution de certaines grandeurs statistiques au voisinage du seuil de
percolation. La caractéristique principale de ces lois d'échelle est leur universalité,
car les exposants qui sont liés à chacune d'entre elles ne dépendent que de la dimension du
problème et pas des détails du réseau (Kesten, 1987, p. 1239).
Résultats dans le réseau de Bethe
Dans le réseau de Bethe, il est possible de déterminer de façon exacte la valeur du seuil de
percolation pc = 1 / (z – 1), avec z le nombre de voisins par site
(§ 1.3.3, p. ??). Ce réseau particulier autorise
aussi la détermination des grandeurs caractéristiques d'un problème de percolation.
Le réseau de Bethe est une structure sans boucle où z branches partent d'un point
origine38. Sur la première couronne, c'est-à-dire
la première génération de voisins de l'origine, on trouve z sites. De chacun de ces sites partent
(z – 1) nouvelles branches qui correspondent alors à des « sous-branches » de l'origine
(figure 1.36).
Figure 1.36: Structure du réseau de Bethe
 |
| Source : Stauffer et Aharony (1992), p. 29 |
Sur la deuxième couronne, il existe par conséquent z (z – 1) sites. La distance euclidienne r n'a pas de
signification dans cette structure et le réseau se décrit alors par la distance chimique l entre deux
sites. Un site sur la l-ième couronne se trouve ainsi à une distance chimique l de
l'origine. Sur cette l-ième couronne, le réseau possède z (z – 1)l – 1 sites. En dimension euclidienne d finie, le
nombre de sites augmente par conséquent de façon exponentielle sur chaque couronne l, selon ld – 1. De là, le
réseau de Bethe peut être considéré comme un réseau de dimension infinie. Suivant les propriétés
d'universalité, les exposants obtenus dans le réseau de Bethe s'appliquent dès lors à tous les réseaux de
dimension infinie (Bunde et Havlin, 1991, p. 67). La dimension critique semble être dc = 6 pour les
phénomènes de percolation39. Selon cette
hypothèse, l'ensemble des réseaux de dimension d ³ 6 auraient des exposants de valeurs identiques à ceux du
réseau de Bethe.
La fonction de corrélation g(l) correspond au nombre moyen de sites dans le même amas et à une
distance l d'un site arbitraire. Pour que deux sites actifs soient à une distance l, il faut
que les l – 1 sites qui les séparent soient également actifs. Chaque couronne possède z
(z – 1)l – 1 sites et l'activité de chaque site est indépendante. Ceci se traduit par (Bunde et
Havlin, 1991, p. 68) :
g(
l) =
z (
z – 1)
l – 1 pl
(18)
À partir de (18), on calcule la longueur de corrélation xl dans
l'espace l :
L'exposant de corrélation dans l'espace l est alors égal à 1.
Le calcul de la taille moyenne des amas finis est obtenu par la relation :
En substituant (18) dans (20), ceci se transforme en :
En conséquences, l'exposant g est égal à un dans le réseau de Bethe.
Concernant le nombre d'amas de taille s normalisé par site ns (p), il est tout d'abord
nécessaire de revenir sur la notion de périmètre en tenant compte des singularités du réseau
étudié. Dans le réseau de Bethe et contrairement au réseau carré (voir § 1.4.1,
p. ??), il existe une relation simple entre le nombre s de sites dans un
amas et le nombre t de sites dans le périmètre (Bunde et Havlin, 1991, p. 69) :
t(s) = z + (s – 1) (z – 2)
(22)
De là, le calcul du nombre d'amas de taille s est simplifié par rapport à l'équation générale
(4) :
ns (p) = gs ps (1 – p)2 + (z – 2) s
(23)
avec gs le nombre de configurations possibles d'un amas de s sites.
Pour étudier le comportement de ns au voisinage du seuil, il est nécessaire de développer p
(1 – p)z – 2 autour de pc = 1 / (z – 1), c'est-à-dire :
ns (
p) ~
ns (
pc)
fs (
p)
(24)
où fs (p) = (1 – [(p – pc)2 / 2 pc2 (1 – pc)])s. Lorsque s augmente, fs (p) décroît
de façon exponentielle. Autrement dit, fs (p) = exp(– c s) avec c ~ (p – pc)2. Au
voisinage du seuil, fs (p) est ainsi une fonction qui ne dépend que de la variable combinée (p
– pc) ss, avec s = 1/2. La dérivation montre que ce résultat est valide lorsque
p tend vers pc par valeur inférieure ou supérieure. Par conséquent, l'exposant s décrit
la vitesse à laquelle le nombre d'amas de taille s décroît en fonction de s, lorsque p est au
dessus ou au dessous du seuil. Dans le réseau de Bethe, il est possible de calculer de façon exacte
le nombre gs de configurations des amas et par la même occasion de déterminer ns (pc). Une
autre approche consiste à supposer que ns (pc) suit une loi puissance (Fisher M.E., 1967,
repris dans Bunde et Havlin, 1991, p. 69) :
L'exposant t s'obtient à partir de (11) et (24) :
|
S = |
|
|
|
s2 ns (p) ~ |
|
s2 – t e– cs ~
|
|
s2 – t e– cs d s
(26) |
|
S ~ ct – 3 |
|
z2 – t e– z d z
(27) |
La probabilité P¥ d'appartenir à l'amas infini est en relation avec ns. En effet,
chaque site dans le réseau est soit inactif avec la probabilité (1 – p), soit actif et membre de
l'amas infini avec la probabilité p P¥, soit actif sans faire partie de l'amas percolant
avec la probabilité p (1 – P¥) º ås s ns :
|
(1 – p) + p P¥ + p |
|
s ns = 1
(29) |
|
P¥ = |
|
|
|
s (ns (pc ) – ns (p)) + (p – pc ) /p
(31) |
P¥ ~ ct – 2 + const × (p – pc )
(32)
De (24) on détermine c. Il est alors possible de calculer la valeur de
l'exposant b :
En substituant t = 5/2 et s = 1/2 dans (33), on obtient b = 1
dans le réseau de Bethe.
De (11) et (30), on remarque que la taille moyenne des
amas finis et la probabilité d'appartenir à l'amas infini sont respectivement le second et le
premier moment de la fonction de distribution des amas ns (p). Le moment zéro, ( M0 º
ås ns ) correspond au nombre moyen d'amas normalisé par site. Pour être de l'ordre de |p – pc|, M0 est tel que :
|
M0 º |
|
ns ~ |p – pc|2 – a
(34) |
Dans le réseau de Bethe, contrairement à la valeur du seuil de percolation, les divers exposants
qui ont été évoqués (a, b, g, s et t) sont indépendants de z. Ce
fait rend compte du caractère universel des exposants critiques liés aux comportements
d'échelle des grandeurs statistiques au voisinage de pc. Ces exposants ont également montré
certaines interrelations. Nous allons à présent revenir sur ces relations ainsi que sur le résultat
des estimations de ces exposants critiques.
Exposants critiques : relations et valeurs estimées
Les exposants critiques attachés aux lois d'échelles ne sont pas indépendants (Sahimi, 1994, p. 16
; Kesten, 1987, p. 1240). La théorie physique d'échelle suppose que ces exposants sont
interdépendants selon deux types de relations : les relations d'échelle et les
relations d'hyper-échelle40.
Les relations d'échelle sont les équations de correspondance entre exposants. Certaines d'entre
elles ont déjà été évoquées pour le réseau de Bethe (voir § 1.4.2,
pp. ??-??) mais elles sont également valides
dans l'ensemble des réseaux :
Il existe d'autres relations comme (Stauffer et Aharony, 1992, pp. 38-39) :
La validité de ces relations d'échelle n'est généralement pas contestée (Grimmett, 1989, p. 151).
Elles montrent ainsi que tout dépend de deux exposants, peu importe qu'il s'agisse de s et
t, ou b et g car de ces deux exposants il est possible de déduire tous les autres
(Stauffer et Aharony, 1992, p. 40). De (38) par exemple, on détermine
a à partir de b et g. Ces relations d'échelle sont utilisées depuis 1960 dans
les problème de transition de phase thermique. Elles ont été étendues à la percolation en 1969 par
P.W. KASTELEYN et C.M. FORTUIN41.
Les relations d'hyper-échelle sont plus discutables42. Elles associent les exposants à la
dimension du problème. À titre d'exemple, on peut citer la relation (Grimmett, 1989, p. 153) :
Les lois d'hyper-échelle ne sont supposées valides que pour des dimensions inférieures à dc la
dimension critique. Pour des dimensions d ³ dc, le processus de percolation semble se
comporter de la même façon que dans un arbre régulier de taille infinie (voir
§ 1.4.2, p. ??).
Les lois d'échelle et d'hyper-échelle peuvent se combiner pour déterminer la valeur des exposants.
Le tableau 1.8 reprend les résultats des estimations pour divers exposants
critiques, dans le problème basique de percolation, où l'activité d'un site est aléatoire et
indépendante de celle des autres sites.
Table 1.8: Valeurs des exposants critiques pour le modèle basique
|
| Exposant |
d = 2 |
d = 3 |
d = 4 |
d = 5 |
d = 6 – e |
Bethe |
|
| a |
– 2/3 |
– 0.62 |
– 0.72 |
– 0.86 |
– 1 + e /7 |
– 1 |
| b |
5/36 |
0.41 |
0.64 |
0.84 |
1 – e /7 |
1 |
| g |
43/18 |
1.80 |
1.44 |
1.18 |
1 + e /7 |
1 |
| n |
4/3 |
0.88 |
0.68 |
0.57 |
1/2 + 5e /84 |
1/2 |
| s |
36/91 |
0.45 |
0.48 |
0.49 |
1/2 + O (e2) |
1/2 |
| t |
187/91 |
2.18 |
2.31 |
2.41 |
5/2 – 3 e /14 |
5/2 |
|
| Source : Stauffer et Aharony (1992), p. 52 |
Comme pour la détermination du seuil de percolation, ces résultats ont été obtenus par le calcul lorsque cela était
possible ou par des estimations (voir § 1.3.3). Les nombres rationnels sont des résultats exacts et ceux
ayant au moins une décimale sont des estimations numériques (Stauffer et Aharony, 1992, p. 52). Ces valeurs sont à
l'origine de classes d'universalité. Ainsi, lorsque deux phénomènes sont décrits par deux ensembles
d'exposants différents, ils sont considérés comme appartenant à des classes d'universalité différentes (Sahimi, 1994,
p. 16). Par conséquent, les lois physiques qui gouvernent les deux phénomènes sont elles aussi considérées distinctes.
Ceci fournit un outil pour comparer un problème au modèle de base ou à un autre modèle.
De façon symétrique, si deux modèles ne suivent pas les mêmes règles, ils n'appartiennent pas à la
même classe d'universalité. Le modèle basique suppose que l'activité d'un site est aléatoire et
statistiquement indépendante de celle des autres sites. Si dans la même structure l'activité des
sites dépend par exemple de l'activité d'un ou plusieurs sites (voisins ou autres), la classe
d'universalité des deux modèles n'est alors plus la même. Les exposants liés au comportement des
grandeurs statistiques observées sur le réseau seront par conséquent différents de ceux du
tableau 1.8.
Au travers de ce paragraphe, les grandeurs macroscopiques telles que la longueur de corrélation, la probabilité
d'appartenir à l'amas infini, la taille moyenne des amas finis et le nombre d'amas de taille s normalisé par site,
ont montré une évolution sous la forme de fonctions puissances de (p – pc) ou |p – pc| au voisinage de pc. À
chacune de ces fonctions, nommées lois d'échelle, est associée un exposant universel. Les relations entre exposants du
type loi d'échelle ou loi d'hyper-échelle, ont illustré la dépendance des diverses grandeurs les unes par rapport aux
autres. La notion de classe d'universalité a aussi été évoquée en indiquant qu'au voisinage de pc et pour une classe
particulière, les détails microscopiques du réseau était négligés. En conséquence, la valeur des exposants critiques
n'est apparue dépendre que de la dimension du problème et pas de la forme de la structure sur laquelle se posait le
modèle. Cette dimension euclidienne d qui a été utilisée jusqu'à présent, n'est cependant pas la seule dimension liée
à la notion de percolation. En effet, certaines propriétés structurelles proviennent de la géométrie fractale et
possèdent une dimension fractale.
1.4.3 Géométrie fractale et percolation
La complexité de certains objets naturels ne peut être décrite par les outils de la géométrie
classique. Pour les modéliser, il est alors nécessaire d'utiliser la géométrie fractale. En théorie
de la percolation, elle permet de préciser certaines caractéristiques qui dépassent la géométrie
traditionnelle. Après avoir explicité la notion de fractale, nous verrons la dimension qui est
associée à l'amas percolant, puis celle liée au graphe lui-même et enfin celle qui correspond aux
sous-structures de la représentation.
Notion de fractale
B. MANDELBROT est à l'origine de la théorie fractale moderne. En 1975, il crée le néologisme
fractale, diminutif de « dimension fractionnaire », qui s'associe à un ensemble
mathématique ou à un objet physique fractal43. Selon ses propres
termes, l'adjectif fractal est employé dans le cas (Mandelbrot, 1995, p. 154) :
« [...] d'une figure géométrique ou d'un objet naturel qui combine les caractéristiques que
voici. A) Ses parties ont la même forme ou structure que le tout, à ceci près qu'elles sont à une
échelle différente et peuvent être légèrement déformées. B) Sa forme est, soit extrêmement
irrégulière, soit extrêmement interrompue ou fragmentée, quelle que soit l'échelle d'examen. C) Il
contient des "éléments distinctifs" dont les échelles sont très variées et
couvrent une très large gamme. »
Pour illustrer un des aspect de la géométrie fractale, B. MANDELBROT pose la question de la
longueur de la côte bretonne (Mandelbrot, 1995, pp. 20-32). Il envisage
de la mesurer sur une carte de France avec un double décimètre et obtient une première estimation.
Suivant le même procédé mais en utilisant une carte d'état-major, le résultat s'accroît. En
parcourant la côte à pied, la longueur de la côte augmente encore car il devient nécessaire de
faire le tour des rochers qui n'existaient pas sur les cartes. À l'échelle d'une fourmi, la côte
bretonne deviendrait gigantesque car l'insecte devrait tenir compte de l'irrégularité de la moindre
pierre. Cette expérience illustre parfaitement le fait que la longueur soit variable et relative à
l'échelle utilisée pour la mesurer. La variation de cette longueur approchée, notée L(h), en
fonction de l'unité d'échelle h a été étudiée par L.F. RICHARDSON en 1961 (Mandelbrot,
1995, p. 22). Cette analyse montre que L(h) est proportionnel à ha où l'exposant
a dépend de la côte étudiée. C'est B. MANDELBROT qui par la suite a interprété
1 + a comme une dimension fractale44.
Pour des objets géométriques classiques, il est très simple de calculer la dimension fractale qui
les caractérise45.
Un segment peut être divisé en N parties égales. Ces N parties correspondent au segment initial
réduit par un facteur d'échelle r = 1/N. Dans ce cas, la relation entre r et N est triviale :
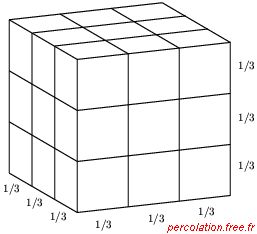
N r = 1. Sur la figure 1.37 (a) par exemple, le segment est coupé en trois
parties, soit N = 3.
Figure 1.37: Dimension fractale pour trois objets géométriques classiques
| (a) Segment |
|
(b) Carré |
|
(c) Cube |
 |
|
 |
|
 |
Le facteur de réduction est alors r = 1/3 et la relation N r = (3) (1/3) = 1, est vérifiée. De
même que pour un segment, les côtés d'un carré peuvent être divisés en parties égales afin
d'obtenir N carrés identiques au carré initial à un facteur d'échelle près. La relation entre r
et N est dans ce cas : N r2 = 1. Sur la figure 1.37 (b) par exemple, les côtés
des carrés sont divisés en trois parties, soit un facteur de réduction pour chaque côté de r = 1/3.
La transformation d'échelle amène à N = 9 carrés et la relation N r2 = (9) (1/9) = 1 se vérifie.
Enfin, si les trois côtés d'un cubes sont réduits d'un facteur r pour obtenir N cubes
identiques, la relation est : N r3 = 1. Dans l'exemple de figure 1.37 (c), le
facteur de réduction est r = 1/3, et le nombre de cubes engendré est N = 27. La relation N r3 =
(27) (1/27) = 1 est alors satisfaite.
Selon la géométrie ordinaire, les objets simples étudiés ci-dessus ont des dimensions entières : le
segment, le carré et le cube sont respectivement de dimension 1, 2 et 3. De plus, ces dimensions
apparaissent de façon systématique comme l'exposant D de la relation N rD = 1, où N est le
nombre de sous-unités égales et r le facteur d'échelle. Ainsi et de façon générale, pour un
ensemble formé de N copies de l'original réduites par un facteur d'échelle constant r, la
valeur Ds qui vérifie la relation N rDs = 1 correspond à la dimension fractale ou
dimension d'homothétie interne de l'ensemble46. La formule qui exprime Ds en fonction du facteur de réduction r
et du facteur du nombre d'éléments N est :
Trouver les mêmes éléments géométriques à différentes échelles est l'une des caractéristiques des fractales appelée
self-similarité ou homothétie interne47. De façon
plus précise, la self-similarité se définit comme l'invariance des propriétés géométriques d'un objet aux
transformations d'échelles homothétiques. La « courbe de von Koch », construite en 1904 par H. VON KOCH,
est l'exemple classique d'une courbe continue non rectifiable à homothétie interne (Mandelbrot, 1995, p. 34). Son
élaboration consiste à itérer une application définie par un générateur sur un initiateur. Dans le
cas de la courbe de von Koch, l'initiateur correspond à un segment (
 ) et le générateur à un segment de
même taille, dont le tiers central est remplacé par deux petits segments joints de taille égale au segment central
supprimé (
) et le générateur à un segment de
même taille, dont le tiers central est remplacé par deux petits segments joints de taille égale au segment central
supprimé (  ). Formellement, ceci
se traduit par un facteur de réduction r = 1/3 et un facteur du nombre d'éléments N = 4. En conséquence, la courbe de
von Koch a pour dimension fractale Ds = log(1/4) / log(1/3) ~ 1,26186.
). Formellement, ceci
se traduit par un facteur de réduction r = 1/3 et un facteur du nombre d'éléments N = 4. En conséquence, la courbe de
von Koch a pour dimension fractale Ds = log(1/4) / log(1/3) ~ 1,26186.
La notion mathématique de dimension fait référence au nombre de vecteurs composant une base
d'espace vectoriel. De façon intuitive, la dimension peut s'interpréter comme le nombre minimal de
déplacements standards pouvant décomposer un mouvement quelconque : le point qui ne permet aucun
déplacement est de dimension zéro, la droite qui ne permet que le glissement est de dimension un,
le plan est de dimension deux, l'espace physique est de dimension trois, etc. La dimension fractale
de la courbe de von Koch Ds ~ 1,26 indique que l'objet représenté n'est plus vraiment une
ligne et pas tout à fait une surface (figure 1.38).
Figure 1.38: Une partie de la courbe de von Koch
 |
| Source : Frankhauser (1994), p. 44
(réalisé avec l'extension fractals.nb, voir note de bas de page n° 1.4.3, p. ??) |
L'intérieur de cette courbe est appelée « flocon de neige » ou « île de von Koch ». Le stade
initial de l'île de von Koch est un triangle. À chaque itération, on applique la transformation
définie par le générateur de la courbe de von Koch en remplaçant chaque partie droite (Frankhauser,
1994, p. 44). Les quatre premières étapes de la construction sont illustrées sur la
figure 1.39.
L'île de von Koch a un périmètre de taille infinie. Ceci se vérifie en étudiant séparément les
côtés du triangle initial. En supposant que chaque segment initial K0 est de taille 1, la courbe
K1 obtenue après transformation est de taille 4/3. La courbe K2 obtenue à la deuxième
itération est de taille 42 / 32. De façon successive, à la n-ième itération la taille de la
courbe Kn est 4n / 3n º (4/3)n. Lorsque n tend vers l'infini, la taille de la courbe
Kn, et par conséquent celle du périmètre de l'île, tend vers l'infini.
Le tapis de Sierpinski est une autre structure fractale régulière. Le procédé de
construction diffère cependant. À l'inverse de la courbe de von Koch, la construction du tapis de
Sierpinski supprime un élément à chaque itération. Le nombre de reproductions de l'objet initial
diminue ainsi à chaque étape. En joignant les milieux des côtés d'un triangle plein, il se divise
en quatre triangles pleins équilatéraux. Le triangle se trouvant à l'intérieur du triangle initial
est vidé. La figure 1.40 illustre l'opération lorsque qu'elle est réitérée quatre
fois.
La transformation se traduit formellement par r = 1/2 et N = 3 car chaque côté du triangle est
divisé par deux et parce qu'un triangle plein donne naissance à trois autres triangles pleins. La
dimension fractale du tapis de Sierpinski est Ds = log(1/3) / log(1/2) ~ 1,58496.
Dans un volume, le procédé de suppression itérative d'une partie de l'objet de départ engendre un
objet appelé éponge de Menger. La figure 1.41 montre les trois premières
étapes de la construction de l'éponge de Menger dans un cube.
Pour cette fractale self-similaire, N = 20 et r = 1/3 dans les trois directions x, y et z. La
dimension fractale de l'éponge de Menger est alors Ds = log(1/20) / log(1/3) ~ 2,72683.
On notera que chaque face de cette éponge correspond à un tapis de Sierpinski itéré sur une base
carrée.
Il est relativement simple de calculer la dimension d'homothétie interne pour des objets obtenus
par itérations successives, mais cette méthode mise en évidence pour des fractales régulières n'est
pas applicable pour des fractales comme celles de la figure 1.42.
Figure 1.42: Exemples de fractales irrégulières
| (a) Vol brownien fractionnaire |
(b) Côte imaginaire |
(c) Continent imaginaire |
 |
 |
 |
| Source : adapté de Mandelbrot (1995), p. 115, p. 119 et p. 121 |
| (a) et (b) réalisés avec un applet Java (disponible en ligne sur
http://polymer.bu.edu/java/) |
| (c) réalisé avec l'extension Fractals.nb de R. WILDER (disponible en ligne
sur http://www.mathsource.com) |
Ces objets appartiennent à la classe des fractales irrégulières, également appelées
fractales aléatoires.
Le calcul de la dimension d'homothétie interne pour des fractales irrégulières peut s'effectuer
selon plusieurs méthodes dont l'une a été évoquée pour mesurer la côte bretonne
(p. ??). Différentes unités d'échelles sont utilisées pour mesurer la
longueur d'une courbe avec des segments de taille identique. Une relation permet ensuite d'estimer
D à partir de ces résultats48. Un autre algorithme
standard pour l'analyse fractale fonctionne par le biais de quadrillages successifs de l'objet.
Cette technique de quadrillage à résolution variable est appelée « comptage de boîtes » (box-counting). Elle
mesure pour différentes échelles, le nombre de boîtes nécessaires à la couverture d'un objet. La longueur N de cet
objet varie en fonction de la taille l du côté des boîtes. Une relation du type ( N = const l– D )
permet ensuite de calculer la dimension d'homothétie interne de l'objet analysé. À titre d'illustration, l'exemple de
trois quadrillages à des échelles différentes est représenté sur la figure 1.43.
Figure 1.43: Quadrillage d'une côte imaginaire à diverses échelles
| (a) l = 100 et N = 13 |
(b) l = 50 et N = 26 |
(c) l = 10 et N = 161 |
 |
 |
 |
| (Réalisé avec un applet Java disponible en ligne sur
http://polymer.bu.edu/java/) |
L'objectif étant de calculer la dimension fractale d'une côte imaginaire en deux dimensions, les
boîtes sont en l'occurrence des carrés de côté l. Dix échelles ont été utilisées de façon
successive. Le nombre de carrés nécessaires pour recouvrir la ligne côtière a été calculé pour
chaque quadrillage49. Les résultats
sont résumés dans le tableau 1.9 et repris graphiquement sur la
figure 1.44.
Table 1.9: Résultats du découpage de la côte imaginaire
| Taille des carrés (l) |
Nombre de carrés (N) |
| 10 |
161 |
| 20 |
74 |
| 30 |
48 |
| 40 |
31 |
| 50 |
26 |
| 60 |
20 |
| 70 |
16 |
| 80 |
13 |
| 90 |
14 |
| 100 |
13 |
Figure 1.44: Résultats graphiques du découpage de la côte imaginaire
Sur la représentation bi-logarithmique du nombre N de carrés en fonction de leur taille unitaire
l, il apparaît clairement que les points obtenus se groupent de manière satisfaisante autour
d'une droite d'ajustement. Dans ces conditions, l'hypothèse d'une fractalité peut alors être
acceptée (Frankhauser, 1994, p. 77). La valeur de la pente permet de déterminer la dimension
d'homothétie interne de la ligne côtière. La dimension fractale correspond à D = – pente,
c'est-à-dire D = 1,145 pour la côte imaginaire de la figure 1.43.
Cette méthode de comptage de boîtes est particulièrement bien adaptée à l'étude de structures
numériques. Il existe cependant un problème pratique lié au découpage, lorsque l'écartement des
mailles ne permet pas de couvrir l'objet de façon précise. Par exemple, le découpage d'un objet de
200 pixels de longueur en boîtes de 50 pixels, se fait précisément avec 4 carrés. Le même objet
découpé en mailles de 55 pixels exige aussi 4 carrés, mais la surface couverte est en réalité de
220 pixels de long. Cette une des raisons pour lesquelles dans le tableau 1.9,
le nombre de carrés nécessaires pour le découpage l = 80 est inférieur à celui calculé pour l = 90.
Dans la mesure du possible, il est préférable de choisir la taille des carrés telle que la fenêtre
d'analyse soit recouverte de façon exacte.
En résumé, la géométrie fractale s'associe à la notion de self-similarité, c'est-à-dire à
l'homothétie interne de la structure d'un objet. Elle met aussi en évidence des relations
puissances entre les variables de taille (longueur, surface ou volume) et les variables d'échelle.
Enfin, elle se caractérise par une dimension géométrique non-entière : la dimension fractale.
Appliquée à la percolation, la géométrie fractale fournit un cadre d'analyse supplémentaire pour
l'étude de certaines grandeurs statistiques.
Dimension fractale de l'amas infini
En percolation, la structure des amas peut se décrire de façon efficace avec le concept de fractale
(Stanley, 1977, repris dans Bunde et Havlin, 1991, p. 58). Au seuil de percolation, l'amas infini
contient des « trous » de différentes tailles formés par les sites absents ou inactifs. La
figure 1.45 illustre l'aspect self-similaire de l'amas percolant à pc.
Figure 1.45: Self-similarité de l'amas percolant au seuil de percolation
| (a) |
(b) |
(c) |
 |
 |
 |
| (amas de taille 7363 sites) |
En d'autres termes, on retrouve les mêmes propriétés géométriques à toutes les échelles supérieures
à l'unité et inférieures à la taille du réseau. En ce sens, l'amas infini correspond à une
fractale.
La dimension fractale Df de l'amas percolant décrit comment en moyenne,
la masse M de l'amas évolue dans une sphère de rayon r telle que :
Pour les fractales aléatoires, M(r) s'obtient par deux méthodes équivalentes. La première
consiste à effectuer une moyenne de la masse des sphères issues d'un même point origine pour de
multiples configurations de l'amas infini. La seconde méthode passe par une moyenne de la masse sur
un même amas percolant, de nombreuses sphères ayant des points origines différents.
La longueur de corrélation x(p) s'interprète comme l'échelle maximale
d'observation pour laquelle l'amas apparaît self-similaire (Bunde et Havlin, 1991, p. 58). En
effet, pour des échelles supérieures à x, la structure n'a plus d'homothétie interne et peut
alors être considérée homogène. Cette modification apparaît clairement sur la
figure 1.46 qui représente un réseau formé de tapis de Sierpinski.
Figure 1.46: Réseau formé de tapis de Sierpinski de taille x
 |
| Source : Bunde et Havlin (1991), p. 59 |
Pour des échelles de taille inférieure à x, la structure apparaît fractale alors que pour une échelle plus grande,
le réseau se présente comme un système homogène composé de cellules de taille x. Formellement, ceci se traduit par
(Bunde et Havlin, 1991, p. 59) :
Il est possible de relier la dimension fractale Df de l'amas percolant aux exposants universels
b et n des lois d'échelle (voir § 1.4.2). En effet, la probabilité qu'un
site arbitraire à l'intérieur d'une sphère de rayon r inférieur à x, appartienne à l'amas
infini se calcule en rapportant le nombre de sites éléments de cet amas au nombre total de sites.
Formellement cette probabilité se définit par :
Cette équation est exacte de façon certaine pour r = a x, où a est une variable constante
inférieure à 1. En substituant r = a x dans (43), l'équation se transforme en
(Bunde et Havlin, 1991, p. 60) :
Enfin, la substitution de (7) et (15) dans
(44) amène à la relation :
La dimension d'homothétie interne Df dépend ainsi des exposants universels b et n, ce
qui permet de conclure que Df possède également la propriété d'être universelle. La
figure 1.47 combine la taille S¥ du plus grand amas d'un réseau
triangulaire au seuil de percolation, à la dimension linéaire L de ce réseau.
Figure 1.47: Taille du plus grand amas au seuil et dimension linéaire du réseau
 |
| Source : Stauffer et Aharony (1992), p. 66 |
Avec une échelle bi-logarithmique, les données montrent un comportement linéaire lorsque L prend des valeurs
importantes. La pente de cette droite de régression est Df = 91/48, ce qui est en accord avec
(45) (Stauffer et Aharony, 1992, p. 66).
Dimension du graphe
La dimension fractale Df n'est pas suffisante pour pouvoir pleinement décrire les amas de percolation. En effet,
d'autres structures peuvent avoir des dimensions fractales comparables mais des caractéristiques différentes. Les
agrégats obtenus en trois dimensions avec un modèle d'agrégation par diffusion limitée (diffusion-limited
aggregation : DLA) ont par exemple une dimension fractale comparable (Df @ 2,5) à celle des amas d'un modèle de
percolation (Bunde et Havlin, 1991, p. 61). Cependant, alors que la structure des seconds révèle de nombreuses boucles,
celle des agrégats de DLA n'en possède quasiment pas. Pour distinguer ces structures, une méthode consiste alors à
s'intéresser à la dimension Dl du graphe.
La longueur l du chemin le plus court entre deux points d'un même amas est appelé
distance chimique50. La dimension Dl du graphe, qui est
aussi qualifiée de dimension chimique ou topologique, associe la masse M de
l'amas à la distance chimique l d'un site donné (Bunde et Havlin, 1991, p. 62) :
Pour un site particulier, M(l) s'obtient en comptant le nombre de sites se trouvant dans le même
amas et dont le chemin d'accès (la distance chimique) est inférieur ou égal à l. De même que pour
M(r), une moyenne doit être faite soit pour un point sur de nombreuses simulations, soit sur de
nombreux points pour une même simulation.
Une relation entre la distance chimique (l) de deux sites et la distance euclidienne (r) de ces
deux sites est obtenue à partir de (41) et (46) :
Si l'on définit Dmin = 1/ n , la relation (47) se transforme en :
l ~ rDmin
(48)
où Dmin s'interprète comme la dimension fractale du chemin le plus court entre deux sites.
Pour reprendre la comparaison entre les agrégats de DLA et les amas de percolation, la valeur de
n en dimension trois, est respectivement 1 pour les premiers et environ 0.75 pour les
seconds. Ainsi, par l'utilisation de Dl ou n, il est possible d'établir des
comparaisons entre les structures fractales lorsqu'elles ont une même dimension d'homothétie
interne Df. Cependant, alors que la valeur de Df était liée aux exposants universels (voir
(45)), une telle relation n'a pas pu être mise en évidence pour la dimension
du graphe Dl. On notera de plus que les valeurs de Dl ou n ne peuvent être
calculées que par des méthodes d'approximation et de simulations numériques.
Sous-structures fractales
De nombreuses sous-structures existent en percolation. Ces
sous-structures s'identifient par les les éléments qui les composent (voir
§ 1.2.2, p. ??, et § 1.4.1,
??). Dans le cas d'un réseau électrique, l'épine dorsale est
formée par les éléments à travers lesquels un flux de courant peut circuler. Les bras
morts sont les éléments qui ne modifient pas la conductance. Les éléments sensibles sont
ceux à travers lesquels transite la totalité du courant et dont la suppression fragmente l'amas
infini. Enfin, les « blocs » (blobs) sont les éléments de l'épine dorsale qui ne sont
pas sensibles.
D'autres sous-structures peuvent aussi être mise en évidence. Parmi elles, on trouve l'« enveloppe
externe » (hull). Il correspond aux sites de l'amas infini qui sont adjacents à des sites
inactifs au « bord » de l'amas, contrairement au périmètre global qui tient compte aussi
des trous à l'intérieur de l'amas. Le squelette est composé par tous les plus courts
chemins d'un site donné vers l'ensemble des sites à une distance chimique l51. Enfin,
l'épine dorsale élastique correspond à l'union des chemins les plus courts entre deux
sites.
Ces sous-structures possèdent comme l'amas infini, la propriété d'être des fractales. Puisqu'une
grande partie de l'amas percolant est formée par des bras morts, la dimension d'homothétie interne
de l'épine dorsale (DB) est inférieure à celle de l'amas percolant (Df)52. La valeur de DB ne peut être obtenue
que par simulation numérique. Au contraire, la dimension fractale des liens sensibles
(Dred) peut être calculée de façon analytique53. En effet, le nombre moyen de
liens sensibles nred varie en fonction de p selon (Coniglio, 1982, repris dans Bunde et Havlin, 1991, p. 64) :
nred ~ (p – pc)– 1 ~ x1/ n
(49)
La dimension fractale des liens sensibles est alors (Dred) = 1/ n. En supposant qu'au seuil l'amas
percolant ait une ramification finie, la dimension du squelette est très proche de Dmin = 1/ n. Enfin, la
dimension fractale de l'enveloppe externe a été calculée de façon exacte en dimension deux : Dh = 7/4
54 (Sapoval et alii, 1985, repris dans Bunde et Havlin, 1991, p. 64).
Le tableau 1.10 reprend les valeurs obtenues pour les diverses dimensions
fractales liées aux amas de percolation, selon la dimension euclidienne de l'espace où se pose le
problème.
Table 1.10: Dimensions fractales des sous-structures d'amas en percolation
| Dimensions |
Dimension de l'espace |
| fractales |
d = 2 |
d = 3 |
d ³ 6 |
| Df |
91/48 * |
2.524 ± 0.008 |
4 |
| Dl |
1,678 ± 0,005 |
1.885 ± 0.015 |
2 |
| DB |
1,620 ± 0,02 |
1.740 ± 0.04 |
2 |
| Dred |
3/4 * |
1.143 ± 0.01 |
2 |
| Dh |
7/4 * |
2.548 ± 0.014 |
4 |
| (*) : valeur exacte |
| Source : Bunde et Havlin (1991), p. 65 |
Certaines valeurs sont exactes (*) et d'autres sont des approximations obtenues par
simulation numérique.
Cette section a mis en évidence les principales propriétés d'un problème statique de percolation. Le calcul des
grandeurs caractéristiques est ainsi apparu comme une première source d'information sur les particularités d'un modèle
de percolation. Ces statistiques de base permettent notamment de rendre compte de la « solidité » de l'amas
percolant, du morcellement d'un état, de sa répartition dans le réseau, etc. Ces informations peuvent alors servir de
base à l'élaboration d'actions ou de politiques, dont l'objectif est de modifier l'état du système étudié. Au seuil de
percolation, le comportement de ces grandeurs révèle une évolution originale sous la forme de lois d'échelle. Attachés
à ces lois, les exposants critiques et les relations entre ces exposants ont une nouvelle fois illustrés le caractère
universel de la théorie de la percolation en manifestant une dépendance vis à vis de la dimension du problème et une
indépendance face aux structures microscopiques du système. Enfin, la géométrie fractale est apparue comme une seconde
source de renseignements pour préciser les propriétés d'un modèle de percolation, au travers des dimensions
d'homothétie interne de l'amas percolant, du graphe et des sous-structures du système.




 ) et le générateur à un segment de
même taille, dont le tiers central est remplacé par deux petits segments joints de taille égale au segment central
supprimé (
) et le générateur à un segment de
même taille, dont le tiers central est remplacé par deux petits segments joints de taille égale au segment central
supprimé (  ). Formellement, ceci
se traduit par un facteur de réduction r = 1/3 et un facteur du nombre d'éléments N = 4. En conséquence, la courbe de
von Koch a pour dimension fractale Ds = log(1/4) / log(1/3) ~ 1,26186.
). Formellement, ceci
se traduit par un facteur de réduction r = 1/3 et un facteur du nombre d'éléments N = 4. En conséquence, la courbe de
von Koch a pour dimension fractale Ds = log(1/4) / log(1/3) ~ 1,26186.


