2.4 D'autres modèles de percolation
Cette section présente des modèles de percolation qui diffèrent sensiblement du modèle basique présenté dans le
chapitre 1. Le premier de ces modèles envisage le problème de la percolation dans un système continu
(§ 2.4.1). Le deuxième modèle met en évidence un autre type de problématique avec la notion de
premier passage de percolation (§ 2.4.2). Enfin, le troisième modèle s'intéresse aux
questions de percolation en gradient (§ 2.4.3).
2.4.1 Percolation de continuum
À la fin de la section 2.3, la modification du support de la
percolation avait été envisagée au travers des réseaux irréguliers. La modification de la
structure peut également être abordée dans un système continu. Les problèmes de ce type
correspondent au modèle qualifié de « percolation de continuum » (continuum
percolation). Après s'être intéressé au processus de Poisson de manière générale, nous
nous arrêterons plus particulièrement sur le modèle dit du « fromage suisse », puis sur
celui dit de « l'escargot sur un tapis de nénuphars ».
Processus de Poisson
Dans le modèle de percolation discret évoqué précédemment, les sites de la structure étudiée sont
disposés de façon non-aléatoire, aux valeurs entières d'un réseau en d dimensions. Dans les
modèles de percolation de continuum au contraire, la position des sites est aléatoire.
Soit P = {pi}i ³ 1 les points d'un processus de Poisson dans
Rd avec une densité constante l. Soit{Fi}i ³ 1
une séquence de figures indépendantes et identiquement distribuées (i.i.d.),
indépendantes de P. Soit W, l'ensemble Èi = 1¥ (pi
+ Fi) comprenant l'origine 0 du graphe. Dans ce cas, pi + Fi
s'interprète comme la figure Fi après translation de pi. Si l'origine n'appartient
pas à l'ensemble Èi = 1¥ (pi + Fi), alors W est un ensemble
vide. Autrement dit, si Fi est une sphère de centre 0 et de rayon ri,
l'ensemble Èi = 1¥ (pi + Fi) correspond à l'union des sphères
centrées aux points aléatoires pi. Le système ainsi défini devient percolant lorsque
l'ensemble W devient infini. Ce phénomène apparaît pour une valeur précise : la
densité critique lc. De façon formelle, la densité critique se définit
par (Kesten, 1987, p. 1247) :
lc = sup{ l : Pl {W est infini} = 0 }
avec Pl la mesure qui gouverne le modèle lorsque P est de densité
l. Le sens de « W est infini » s'interprète aussi bien comme le fait que « W
soit de volume Euclidien infini » ou que « W contient un nombre infini de pi », car
ces deux interprétations conduisent au même lc (Roy, 1987, repris dans : Kesten,
1987, p. 1247).
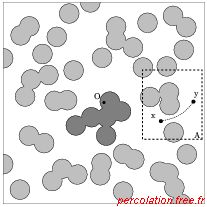
La figure 2.47 illustre un système de percolation de continuum où des disques de
rayon ri sont placés de façon aléatoire dans le plan.
Figure 2.47: Exemple de percolation de continuum en dimension deux
| (a) Disques de rayon identique |
|
(b) Disques de
rayon variable |
 |
|
 |
| Source : adapté de Meester et Roy (1996), p. 15 |
La figure (a) est formée par des disques de rayon identique, alors que sur la figure (b)
leur rayon est variable. Dans les deux cas, l'espace est divisé en deux régions (Meester
et Roy, 1996, p. 15). La région « occupée » constituée par la surface des disques, et la
région « vacante » formant le complément de la région occupée. Sur la
figure 2.47, la région occupée est en gris et la région vacante est en
blanc. L'ensemble W contenant l'origine, est mis en évidence par un gris plus foncé.
Lorsque deux points x et y appartiennent au même composant occupé, ils sont qualifiés
de « connectés dans la région occupée ». Symétriquement, deux points sont dit « connectés
dans la région vacante » lorsqu'ils appartiennent à une même composante vacante
(figures 2.47 (a) et (b)). De là, l'intérêt peut se porter aussi bien
sur la percolation d'un passage entre les sphères que sur les sphères
(Sahimi, 1994, p. 19).
Modèle dit du fromage suisse
Le modèle du fromage suisse (Swiss cheese model) s'intéresse à la percolation d'un chemin
entre les inclusions, c'est-à-dire à la région vacante. En trois dimensions, le système est
représenté en disposant de façon aléatoire des trous sphériques de rayon identique, dans un milieu
uniforme. Les trous ont la possibilité de se chevaucher. De cette façon, le système formé par la
structure vacante autorise le transport, seulement lorsque le volume q occupé par les trous est
inférieur au seuil qc (Stauffer et Aharony, 1992, p. 109).
Le modèle peut être illustré sur un réseau aléatoire, où les liens représentent des «
goulets » dont la présence ou l'absence est déterminée par l'intersection des trous
(Elam, Kerstein et Rehr, 1984, repris dans : Halperin et alii, 1985, p. 2391).
La figure 2.48 montre la représentation du modèle du fromage suisse en
deux dimensions.
Figure 2.48: Modèle du fromage suisse en deux dimensions
 |
| Source : Feng et alii (1987), p. 207 |
Le réseau discret de liens présents est représenté par des segments continus alors que
les liens manquants sont représentés par des pointillés. Le lien entre deux trous voisins
est présent lorsque ceux-ci ne se chevauchent pas et il est absent dans le cas contraire.
Cette construction se base ainsi sur une tesselation où les liens sont définis par les
côtés des polygones de Voronoï 49.
Dans ce modèle du fromage suisse, les exposants critiques des propriétés géométriques, comme par exemple la longueur de
corrélation, sont les mêmes que dans le modèle ordinaire de percolation. Cependant, les exposants liés au comportement
électrique du système apparaissent différents (Halperin et alii, 1985, p. 2393).
En inversant le problème, c'est-à-dire en posant conductrice la région occupée et
isolante la région vacante, le problème se transforme en modèle du fromage suisse
inversé (Feng et alii, 1987, p. 210-211). Le modèle dit de « l'escargot sur un
tapis de nénuphars » montre une autre façon de s'intéresser à la région formée par la
superposition des disques.
Modèle dit de l'escargot sur un tapis de nénuphars
Le principe du modèle dit de « l'escargot sur un tapis de nénuphars » (snail on a
lily pond) est simple. Dans celui-ci, les disques représentent des nénuphars dont la
taille augmente de façon uniforme dans le temps. Le problème de l'escargot est alors de
savoir combien de temps il lui faut attendre, pour qu'un chemin continu de nénuphars lui
permette de traverser l'étang (Grimmett, 1989, p. 250). Formulé différemment, la question
consiste à déterminer la densité minimale de disques qui assurent l'existence d'un amas
percolant dans le plan. La figure 2.49 montre un exemple de trajet effectué
par l'escargot, sur ce tapis de nénuphars.
Figure 2.49: Trajet d'un escargot sur un tapis de nénuphars
 |
| Source : Grimmett (1989), p. 250 |
Les centres des disques sont les points d'un processus de Poisson avec intensité
l dans Rd. Soit g (l) la probabilité de
percolation, il existe alors une valeur critique lc telle que (Grimmett, 1989,
p. 251) :
|
g (l) |
ì
í
î |
| = 0 |
si |
l < lc |
| > 0 |
si |
l > lc |
|
|
(29) |
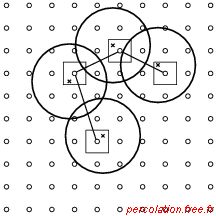
Figure 2.50: Étude du modèle continu dans un réseau discret
 |
| Source : Grimmett (1989), p. 253 |
Les points « ° » représentent les sites qui divisent le réseau plan en carrés. Les
croix indiquent le centre de chaque cercle. Chacune de ces croix est associée avec le
site qui lui est le plus proche (l'association est symbolisée par les carrés). Dans cette
représentation, deux sites sont plus proches voisins lorsque les disques se chevauchent.
Soit n un entier positif et Znd l'ensemble
n– 1 Zd précisant les coordonnées du centre des carrés qui
réalisent la partition de Rd. Les deux sites du réseau discret
représentés sur la figure 2.51 sont des plus proches
voisins, car leur disque respectif se chevauchent lorsque leur rayon est supérieur à 1
+ n– 1 Ö d 50.
Figure 2.51: Liaison de deux sites sur le réseau discret
 |
| Source : Grimmett (1989), p. 255 |
Une fois ce réseau discret obtenu, le problème de l'escargot s'analyse selon la vitesse
avec laquelle le rayon du nénuphar évolue.
Ainsi, le modèle de percolation de continuum s'écarte du modèle ordinaire de percolation posé dans
un réseau discret. La structure, sur laquelle il évolue, n'est alors plus limitée par les
hypothèses de forme du réseau. De cette manière, le modèle de percolation de continuum semble mieux
correspondre à certains phénomènes réels. Cependant, ce développement ne diminue pas l'intérêt du
modèle ordinaire de percolation. Comme cela a été montré avec le modèle de l'escargot sur son tapis
de nénuphars, il est possible d'approximer les problèmes continus par des problèmes discrets.
2.4.2 Premier passage de percolation
Le modèle de « premier passage de percolation » (first-passage percolation) est
un des principaux sujets de développement mathématique en percolation (Smythe, 1983,
p. 479). Il s'interprète comme une généralisation du modèle ordinaire de percolation.
Après avoir exposé les relations que le modèle de premier passage de percolation
entretient avec le modèle basique, son principe général sera présenté de façon formelle.
Pour terminer, la notion de constante de temps sera développée.
Modèle basique versus premier passage de percolation
J.M. HAMMERSLEY et D.J. WELSH ont formulé le problème de premier passage de percolation
en 196351. Contrairement au modèle ordinaire de percolation où à
chaque lien est associée une valeur 0 ou 1, les liens du modèle de premier passage de
percolation prennent n'importe quelle valeur à condition qu'elle soit non négative. Cette
valeur correspond à une mesure de temps et elle caractérise la durée nécessaire pour
traverser le lien. De là, une problématique différente se trouve posée.
La distinction entre les deux modèles peut s'illustrer avec l'exemple de la propagation d'un feu ou
d'une maladie dans un verger (Hammersley et Welsh, 1965, p. 61). Dans le modèle standard de
percolation, les arbres étant placés sur les sites d'un réseau carré, la distance entre les arbres
est supposée telle que la maladie ne puisse être transmise qu'aux quatre plus proches voisins d'un
arbre infecté. La probabilité que chaque arbre soit touché est p, indépendamment de l'état de ses
voisins. La théorie de la percolation renseigne alors sur le probabilité PN (p) pour que la
maladie se propage d'un arbre à plus de N autres arbres. Dans le modèle de premier passage de
percolation, on associe au lien de chaque paire de sites voisins, une valeur aléatoire non
négative, indépendante et identiquement distribuée. Cette valeur s'interprète comme la durée
nécessaire pour qu'un arbre malade infecte le voisin en question. La théorie de la percolation
informe alors sur la durée minimale pour que l'infection se propage en dehors d'une région
particulière.
En fait, les deux modèles ne sont pas incompatibles. Lorsque les liens ont une probabilité p
d'avoir un temps de passage nul et une probabilité 1 – p d'avoir un temps de passage unitaire, le
modèle basique apparaît comme un cas particulier du modèle de premier-passage de percolation. La
probabilité de percolation entre deux sites est alors équivalente à la probabilité pour que le
temps de premier passage de percolation entre les deux sites soit nul (Hammersley et Welsh, 1965,
p. 63). Le modèle de premier passage de percolation se présente ainsi comme une généralisation du
modèle de percolation ordinaire.
Formulation du modèle
De façon plus générale, le problème de premier passage de percolation se pose dans un
graphe formé par un ensemble de sites et de liens (Kesten, 1987, p. 1257). À chaque lien
L de Zd, on associe une variable aléatoire non négative,
indépendante et identiquement distribuée, t(L). Celle-ci s'interprète comme le temps
nécessaire pour traverser le lien L. La loi de distribution des t(L) est notée F.
Le temps de passage T(r) d'un chemin r de Zd, formé
par les liens L1, ..., Ln, se définit par la somme des temps de passage
individuels de chacun de ces liens52. De façon formelle, ceci se traduit par :
Dans ces conditions, la durée du trajet de u à v correspond au temps de
premier passage T(u, v), défini comme la durée minimale pour joindre les deux
éléments parmi l'ensemble des chemins possibles53 :
T(u, v) = inf{T(r) : r est un chemin de u à v }
(31)
Ce temps de premier passage est une variable aléatoire et la distribution de T(u, v) est
fonction de la loi F.
L'ensemble des sites pouvant être atteint au bout d'un temps t à partir de l'origine
0 est noté B (t) :
B (t) = { v Î Zd : T(0, v) £ t }
(32)
Cet ensemble B (t) et ses caractéristiques asymptotiques pour des valeurs de t
importantes, sont les principaux sujets d'analyse du modèle de premier passage de
percolation. Cette problématique peut être mise en parallèle avec les questions d'«
itinéraire optimal », puisqu'un site v n'appartient à l'ensemble B (t) que lorsque le
temps du trajet est inférieur à t.
Afin d'étudier le comportement du système, il est nécessaire de modifier l'échelle
d'analyse. La structure B (t) est alors remplacée par B(t) qui correspond au cube
unitaire centré à l'origine 0. Cette nouvelle structure se définit par
(Kesten, 1987, p. 1258) :
B(t) = { v + U : v Î B (t) }
(33)
avec
|
U = { x = (x(1), ... , x(d)) : |x(i)| £ |
|
, 1 £ i £ d }
|
-
soit B0 est compact avec (1 – e ) B0 Ì 1/t B(t) Ì (1 + e )
B0 de façon presque certaine, pour tout e > 0 ;
- soit B0 = Rd avec 1/t B(t) É { x : |x| £
e– 1 } de façon presque certaine, pour tout e > 0 ;
Le problème est alors de déterminer B0 en fonction de F (la loi de distribution des t(L)) et
de la dimension d. Mis à part l'exemple trivial où F assigne une masse unitaire aux points, le
calcul de B0 ne peut être fait de façon systématique (Kesten, 1987, p. 1259). Lorsque d = 2, il
semble cependant que la frontière de B0 contienne des segments de droite (Durrett et Ligget,
1981, repris dans : Kesten, 1987, p. 1258).
Temps de passage et constante de temps
Pour obtenir des informations sur B0, il est possible d'étudier la position du point
le plus à droite, atteint par le système. De là résultent les notions de temps de passage
« d'un point à un point », notée a0, n et de temps de passage « d'un point à une
droite (ou à un hyperplan) », notée b0, n et définies par (Kesten, 1987, p. 1260)
:
a0, n = T(0, (n, 0, ... , 0)) et b0, n =
T(0, { x : x(1) = n } )
Sous l'hypothèse E [t(L)] < ¥, les temps de passages a0, n et b0, n montrent
une propriété particulière (Kesten, 1987, p. 1260) :
|
|
|
|
|
a0, n = |
|
|
|
b0, n = µ de façon presque certaine
(34) |
µ = µ (F, d)
(35)
Cette propriété de constante de temps avait été suggérée par J.M. HAMMERSLEY et D.J.
WELSH, et elle a été démontrée grâce à un théorème de J.F. KINGMAN (Kingman, 1968, repris
dans : Kesten, 1996, p. 2). Cette constante est l'un des facteurs gouvernant la forme
B0 prise par le système. La façon dont µ évolue en fonction de F et d reste à
ce jour relativement méconnue (Grimmett, 1989, p. 259).
Le modèle de premier passage de percolation est relativement complexe. S'il semble plus général que le modèle ordinaire
de percolation, ses propriétés ne sont pas encore totalement maîtrisées. Il est à noter qu'une relation existe entre le
modèle d'Eden étudié au § 2.2.2, et le modèle de premier passage de percolation54. Ainsi, pour le
modèle de croissance où la probabilité d'ajouter un site à l'amas est proportionnel au nombre de voisins actifs de ce
site, le système obtenu est équivalent à B(t) lorsque la loi de distribution F est exponentielle (Kesten, 1987,
p. 1259). Des extensions au modèle de premier passage de percolation sont également possibles. En ce sens, une nouvelle
famille de modèles peut être proposée sur des structures continues, en utilisant des tesselations de Voronoï (Howard et
Newman, 1997)
2.4.3 Percolation en gradient
Le modèle de percolation en gradient se distingue du modèle traditionnel de percolation. Dans ce
dernier, les éléments actifs sont répartis de façon homogène sur la structure. Dans le modèle de
percolation en gradient, la probabilité d'activité (p) des éléments décroît de façon monotone de
1 à 0, avec la distance x qui les sépare d'un des bords du système. La forme précise de la
variation de p n'est pas importante. L'essentiel est que la dépendance directionnelle amène d'une
activité totale sur la première rangée, à une activité nulle sur la dernière rangée. Ce mécanisme
se retrouve notamment dans les problèmes de fronts de diffusion et de fronts
d'invasion55. Après avoir donné un
exemple de front en deux et trois dimensions, la relation entre le seuil de percolation et le
modèle de gradient de concentration sera présentée. Le troisième point analysera les principales
caractéristiques d'un front de diffusion.
Fronts de diffusion en deux et trois dimensions
Sur une structure de sites, des particules diffusent à partir d'une source associée à un
des bords du réseau. Les particules se déplacent de site en site. Lorsque la probabilité
de diffusion est la même pour l'ensemble des particules, la situation est qualifiée «
sans interaction » (Gouyet, 1992, p. 118). Au contraire, lorsque cette probabilité dépend
des particules voisines, le problème correspond à une situation « avec interaction »,
celle-ci pouvant être attractive ou répulsive. Les illustrations
présentées ici correspondent à des fronts de diffusion sans interaction.
La figure 2.52 (a) montre le front de diffusion (en noir) sur une structure en gradient.
Figure 2.52: Exemple de front de diffusion en deux dimensions
| (a) 256 × 256 sites |
|
(b) Agrandissement |
 |
|
 |
Les particules se diffusent à partir du bord gauche. L'ensemble des sites connectés à la
source (de proche en proche) est représenté en gris foncé. Les sites en gris clair, au
contraire, sont isolés de la source. Le front de diffusion correspond à la surface
externe de l'ensemble des sites connectés de proche en proche, au bord gauche de la
structure (Stauffer et Aharony, 1992, p. 131). La figure (a) ne couvre pas entièrement la
structure en gradient. Seule la zone où p est compris entre 0,8 et 0,3 est représentée.
Ceci explique que la première rangée à gauche ne soit pas uniquement formée par des sites
actifs et la dernière rangée à droite, par des sites inactifs. La
figure 2.52 (b) montre un agrandissement de la zone marquée sur la
figure (a).
La figure 2.53 montre un exemple de front de diffusion en trois dimensions.
Figure 2.53: Exemple de front de diffusion en trois dimensions
Seuls les sites connectés de proche en proche à la source diffusante (la face gauche du
cube sur l'illustration) sont représentés. La structure du front obtenue dans ces
conditions est plus complexe qu'en deux dimensions. Dans le cas où d = 2, le front est
très fortement localisé dans le voisinage du seuil de percolation du graphe, alors que
pour d = 3, le front s'étend sur une région beaucoup plus large. Dans le cas du réseau
cubique simple cette région est comprise entre 0,312 et 0,956.
Seuil de percolation et modèle de gradient de concentration
Le front de diffusion d'un modèle de gradient de concentration est lié au seuil de percolation de sites sur le même
réseau. Pour des systèmes de taille importante (L ® ¥ ), la structure du front de diffusion est
comparable à la structure de l'enveloppe externe d'un amas de percolation. De façon intuitive, le front s'associe à un
amas permettant de joindre les bords opposés de l'échantillon. Le seuil de percolation est alors identique à la
concentration de particules présentes à la position moyenne xf du front (Gouyet et alii, 1991, p. 243) :
L'analyse du front sur une structure carrée, à laquelle est appliquée un gradient de
concentration constant, amène à une estimation très précise du seuil critique. Deux types
d'amas sont différenciés. Les sites actifs forment des amas A, définis par des
connexions entre plus proches voisins (voisinage de von Neumann). Les sites inactifs
constituent des amas B, définis par des liaisons entre proches voisins (voisinage de
Moore). Dans ce contexte, la probabilité de percolation correspond à la probabilité de
concentration minimale nécessaire à l'apparition d'un amas A de taille infinie. De la
sorte, les amas A et B sont définis sur des graphes de coordinence différente. Ces
deux réseaux particuliers constituent une « paire adaptée » (matching
pair)57. Étant donnée la définition des amas, et dans le cas d'un gradient de
concentration monotone allant de 0 à 1, il existe simultanément un amas infini A et un
amas infini B (Rosso et alii, 1985, p. 6053).
Les sites de l'amas infini A qui sont proches voisins des sites de l'amas infini B,
forment le front des sites actifs fA. De façon équivalente, la frontière fB correspond aux
sites de l'amas infini B, plus proches voisins des sites de l'amas infini A. Ces deux
frontières sont représentées sur la figure 2.54.
Figure 2.54: Frontières des sites A et B
 |
| Source : Rosso et alii (1985), p. 6053 |
Pour chaque frontière, la position moyenne xfA et xfB, l'épaisseur
sfA et sfB, ainsi que le nombre de sites NfA et
NfB sont répertoriés. De là, une nouvelle frontière fAB est définie comme
l'union de fA et fB. Sa position xAB correspond à la position moyenne des deux
autres fronts :
|
xfAB = |
| NfA xfA + NfB xfB |
|
| NfA + NfB |
|
Des simulations numériques de ce modèle ont été réalisées, la concentration p(x) de sites A étant donnée par (Rosso
et alii, 1985, p. 6054) :
p(x) = 1 – x |Ñ p |
avec Ñ p la constante du gradient de concentration. La figure 2.55 montre
l'évolution de la concentration critique, en fonction de la valeur de la constante du gradient de
concentration.
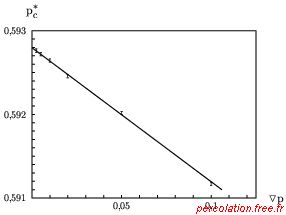
Figure 2.55: Évolution de la concentration critique en fonction du gradient
 |
| Source : Rosso et alii (1985), p. 6054 |
La concentration critique pc* est définie comme la valeur de p à la distance
moyenne xfAB du front. La valeur du seuil est déterminée pour Ñ p = 0. La
valeur obtenue est : pc = 0,592802 ± 10– 5. Cette estimation apparaît comme l'une
des meilleures estimations du seuil de percolation dans le réseau carré de sites.
Caractéristiques du front
Pour caractériser l'interface obtenue avec le modèle de percolation en gradient, on peut tout d'abord rendre compte de
la dimension fractale du front. Des études empiriques et théoriques ont montré que pour d = 2, la dimension fractale
Df du front était liée à l'exposant critique n par la relation (Gouyet et alii, 1991, p. 244) :
Les autres caractéristiques du front de diffusion, son épaisseur sf et sa longueur
Nf (nombre de particules constituant le front), s'expriment en fonction du gradient de
concentration Ñ p = dp/dx (figure 2.56).
Figure 2.56: Profil de concentration et seuil de percolation
 |
| Source : Gouyet (1992), p. 121 |
Pour de faibles concentrations, la taille des amas actifs est réduite. Au voisinage du front au contraire, elle devient
comparable à l'épaisseur du front lui-même. La loi d'échelle associée à la longueur de corrélation indique en ce sens,
que la taille des amas doit augmenter à l'approche de xf, la position moyenne du front58 (Gouyet et alii, 1991, p. 244). Cependant, étant donnée la définition du
gradient p(x), la taille des amas reste bornée, même à xf. Ainsi, la taille maximale des amas est donnée par
l'épaisseur du front qui correspond à la seule longueur caractéristique du problème. Ceci se traduit par (Gouyet
et alii, 1991, p. 245) :
sf ~ x ( xf ± sf )
(38)
De (15) et (36), on obtient alors :
|
sf ~ | p (xf ± sf ) – pc |– n @
|
½
½
½
½ |
sf |
|
(xf) |
½
½
½
½ |
|
|
sf ~ |
½
½
½
½ |
|
(xf) |
½
½
½
½ |
|
avec
as = |
|
(39) |
La longueur du front varie également comme une loi puissance du gradient de concentration. Le nombre de sites d'un
front de dimension linéaire L, dans un carré de coté sf est égal à ( Nf sf ) / L. Le front de
diffusion étant fractal, il suit que Nf ~ L sfDf – 1. La longueur du front évolue alors suivant la
relation (Gouyet et alii, 1991, p. 246) :
|
Nf ~ |
½
½
½
½ |
|
(xf) |
½
½
½
½ |
|
avec
aN = |
|
(40) |
Il est probable, mais non prouvé théoriquement, que les résultats présentés soient universels. Les valeurs de Df,
as et aN seraient par conséquent indépendantes de la structure et entièrement déterminées par la
dimension du problème.
La correspondance existant sous certaines conditions entre les modèles de gradient de
concentration, comme par exemple les fronts de diffusion, et le modèle ordinaire de
percolation a été soulignée dans ce paragraphe. Cette relation amène ainsi à parler de «
modèle de percolation en gradient », lorsque la concentration évolue de façon monotone et
décroissante de 0 à 1. Outre l'intérêt particulier d'un problème de percolation qui peut
amener à considérer un front de diffusion, ce modèle s'est également montré très efficace
dans l'estimation numérique du seuil en deux dimensions.





