2.3 Déformations du modèle basique de percolation
Dans le modèle ordinaire de percolation, l'état d'un élément est indépendant de celui des autres éléments. Se basant
sur un aspect local précis, la théorie de la percolation analyse la façon dont les éléments sont coordonnés les uns aux
autres pour un réseau donné. Les modèles de percolation qui vont être présentés dans le cadre de cette section,
abandonnent tour à tour certains de ces principes. Après nous être intéressés à la modification de la notion de
voisinage (§ 2.3.1), la non-orientation des éléments du système sera remise en question
(§ 2.3.2). Les aspects concernant l'indépendance de l'état des éléments seront ensuite présentés
(§ 2.3.3), avant de terminer en s'attardant sur la question de la structure du réseau
(§ 2.3.4).
2.3.1 Modification du voisinage
L'aspect local, sur lequel repose les relations entre les éléments d'un système, est
décisif dans l'interprétation des résultats du modèle de percolation. Jusqu'à présent, la
contiguïté s'était limitée aux « plus proches voisins ». Ce paragraphe revient en détail
sur différentes formes possibles du voisinage d'un site dans un réseau carré, et en
illustre quelques conséquences à travers la simulation numérique.
Voisinage de von Neumann
Dans le modèle de percolation de sites sur un réseau carré, le voisinage de von Neumann est le plus fréquemment
utilisé. Selon cette règle, un site X donné possède quatre voisins (N, E, S, O) : un dans chaque direction
(figure 2.32 (a)).
Figure 2.32: Voisinage de von Neumann
| (a) Représentation cardinale |
|
(b) Les « plus proches voisins » |
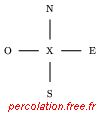 |
|
 |
| Source : Gaylord et Nishidate (1996), p. 4 |
Selon la représentation traditionnelle du réseau carré de sites, ces voisins
correspondent aux cases ayant un côté en commun avec la case de départ. Ces cases,
représentées en gris sur la figure 2.32 (b), désignent le « plus
proche voisinage » du site.
Voisinage de Moore
Le voisinage de Moore est plus large que ne l'est celui de von Neumann. Aux quatre points cardinaux
(N, E, S,O), la règle de Moore ajoute les sites intermédiaires : NE, SE, SO et NO (figure 2.33 (a)).
Figure 2.33: Voisinage de Moore
| (a) Représentation cardinale |
|
(b) Les « proches voisins » |
 |
|
 |
| Source : Gaylord et Nishidate (1996), p. 4 |
La figure 2.33 (b) souligne ce type de voisinage dans le cadre ordinaire
du réseau carré. Dans cette situation, les cases voisines (représentées en gris),
encadrent complètement le site de référence en noir. Ainsi, deux cases sont dites
voisines, au sens de Moore, lorsqu'elles ont un côté ou un coin en commun. Ces éléments
représentent le « proche voisinage » d'un site.
Voisinage de Moore-von Neumann
Le dernier type de voisinage évoqué ici, est une combinaison des deux premiers : le voisinage de Moore-von Neumann.
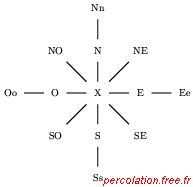
Élargissant encore le nombre de voisins, il intègre les points cardinaux (N, E, S, O), les points
intermédiaires (NE, SE, SO, NO) de la première couronne, ainsi que les points cardinaux de la deuxième
couronne : Nn, Ee, Ss et Oo (figure 2.34 (a)).
Figure 2.34: Voisinage de Moore-von Neumann
| (a) Représentation cardinale |
|
(b) Les « voisins » |
 |
|
 |
| Source : Gaylord et Nishidate (1996), p. 5 |
Dans le contexte Moore-von Neumann, chaque site possède ainsi 12 voisins. Selon la
représentation courante du réseau carré de sites, la
figure 2.34 (b) met en évidence les cases correspondantes. Ainsi,
deux cases sont dites voisines dans trois situations : soit elles ont un côté commun,
soit elles ont un coin commun, soit elles sont séparées horizontalement ou verticalement
par une autre case. Au sens des proches et plus proches voisins, les
sites de Moore-von Neumann correspondent au « voisinage » du site de référence.
D'autres formes de voisinage peuvent être choisies selon le contexte et les caractéristiques du
problème à étudier. De plus, ce principe ne se limite pas à l'unique réseau carré. Le voisinage
peut être modifié de la sorte, quel que soit le type de réseau retenu. Il est cependant fondamental
que la règle de voisinage s'applique de façon uniforme à l'ensemble des éléments du système pour
rester dans le cadre de la percolation. Le point suivant présente les principales conséquences de
la modification du voisinage, à travers les résultats d'une simulation numérique.
Simulations numériques
Quelques effets de la modification du voisinage ont déjà été évoqués avec les modèles de feux de forêt34. La
figure 2.35 (a) montre le résultat d'un problème de percolation standard dans un réseau carré de
sites.
Figure 2.35: Réseau de percolation selon la définition du voisinage
| (a) Réseau initial |
 |
| |
| (b) Voisinage de von Neumann |
(c) Voisinage de Moore |
 |
 |
| (664 amas) |
(56 amas) |
Dans ce réseau aléatoire hétérogène, les sites actifs sont représentés en noir et les
inactifs en blanc. La proportion de sites actifs est p = 0,5 et la taille du réseau est
de 100 × 100 sites. À partir de cette situation initiale, les résultats sont
différents selon la définition du voisinage retenue. Les
figures 2.35 (b) et (c) représentent respectivement, le résultat
d'une analyse en terme de voisinage de von-Neumann et de voisinage de Moore.
Selon le voisinage de von Neumann, il n'existe pas d'amas infini. Le système ne percole pas. Des amas de tailles très
variées sont présents sur l'ensemble du réseau. Au contraire, avec le même réseau mais sous l'hypothèse d'un voisinage
de Moore, un amas percolant apparaît. La plupart des sites actifs appartiennent à cet amas infini représenté en gris
clair sur la figure (c).
Le tableau 2.2 reprend de façon plus complète la statistique des amas.
Table 2.2: Taille et nombre d'amas selon la définition du voisinage
| (a) Voisinage de von Neumann |
|
(b) Voisinage de Moore |
| Taille des amas |
Nombre d'amas |
|
Taille des amas |
Nombre d'amas |
| 1 |
308 |
|
1 |
37 |
| [ 2, 5 ] |
179 |
|
[ 2, 5 ] |
16 |
| [ 6, 10 ] |
71 |
|
[ 6, 10 ] |
2 |
| [ 11, 20 ] |
50 |
|
[ 11, 20 ] |
0 |
| [ 21, 50 ] |
38 |
|
[ 21, 50 ] |
0 |
| [ 51, 100 ] |
13 |
|
[ 51, 100 ] |
0 |
| > 100 |
5 |
|
> 100 |
1 |
| Total : |
664 |
|
Total : |
56 |
| Amas le plus grand : 181 sites |
|
Amas le plus grand : 4 914 sites |
Selon le voisinage de Moore, le nombre de sites actifs isolés, c'est-à-dire les amas de
taille unitaire, sont peu nombreux. La coordinence des sites étant deux fois plus élevée
dans un voisinage à la Moore (z = 8) que dans un voisinage à la von Neumann (z = 4), il
est logique que le nombre d'amas de petite taille soit inférieur. De même, le nombre
total d'amas est plus faible et leur taille est plus importante. De 664 amas, on passe à
56 lorsque la connexion des éléments s'étend jusqu'aux proches voisins. Sur le réseau,
l'amas le plus grand est formé de 181 sites dans le voisinage de von Neumann, alors qu'il
est de 4914 sites dans le voisinage de Moore. Dans ce dernier cas, l'amas correspond à
l'amas infini. Il intègre 98,28 % des sites actifs du système ce qui lui donne une
certaine robustesse.
La coordinence étant différente selon le type de voisinage choisi, le résultat d'un même problème de percolation montre
des réalités différentes, voire opposées. Lorsque la modification de la règle de voisinage est en faveur de son
extension, en passant par exemple du modèle de von Neumann au modèle de Moore, le seuil de percolation diminue. Lorsque
les différentes analyses sont dans une même dimension, elles appartiennent néanmoins à la même classe d'universalité.
Dans ce paragraphe, plusieurs exemples de voisinage ont été présentés dans le réseau carré : voisinage de von Neumann,
de Moore et de Moore-von Neumann. Le choix du voisinage s'est montré déterminant pour analyser la structure du système
: nombre d'amas, tailles, présence d'un amas percolant, etc. Le paragraphe suivant montre un autre type d'extension du
modèle basique de percolation.
2.3.2 Percolation dirigée
Le modèle élémentaire de percolation évolue dans un graphe dont les arêtes sont non orientées. Les propriétés
du système sont alors identiques dans toutes les directions. Le modèle de percolation dirigée, au contraire, introduit
une orientation sur la structure. Le système devient alors anisotrope. Après avoir donné une définition de
l'anisotropie au travers de quelques exemples, les différents types de modèles de percolation dirigée seront évoqués.
Les conséquences de l'anisotropie et les résultats de quelques estimations seront enfin présentés pour le modèle de
percolation entièrement dirigée.
Percolation anisotrope
L'isotropie et l'anisotropie sont des propriétés des corps
macroscopiques35. Lorsque les propriétés
macroscopiques d'un système n'ont pas de dépendance directionnelle, il est qualifié
d'isotrope. Les propriétés sont alors invariantes aux rotations dans le trièdre de
référence (Ox, Oy, Oz). Dès que l'une de ces propriétés est directionnelle,
l'objet macroscopique devient anisotrope. L'invariance n'est alors plus vérifiée pour
l'ensemble des rotations.
Dans le cadre de la percolation, l'anisotropie est principalement étudiée du point de vue des
modèles de liens. Pour affecter une propriété directionnelle au système dans un modèle élémentaire,
il suffit par exemple d'affecter des probabilités d'activité différentes selon la direction. En
dimension deux dans un réseau carré, si la probabilité d'activité pH des liens horizontaux est
différente de la probabilité d'activité pV des liens verticaux, le système est anisotrope.
Dans un réseau triangulaire, on peut envisager des probabilités d'activité p1, p2 et p3
selon que l'inclinaison du lien est de 0, p /3 ou 2p /3 par rapport à l'horizontal. Dans
ces deux exemples, la probabilité critique se transforme en surface critique : j
(p1, p2, ...) (Grimmett, 1989, p. 238). Pour l'exemple du réseau carré, la surface se
définit par j (pH, pV) = pH + pV – 1. Les amas sont de taille finie lorsque j
(pH, pV) < 0, et il existe un amas infini unique si j (pH, pV) > 0. Les mêmes
conclusions s'appliquent à l'exemple du réseau triangulaire, mais la surface critique est définie
par : j (p1, p2, p3) = p1 + p2 + p3 – p1 p2 p3 – 1.
En distinguant les probabilités selon les directions, on peut aussi envisager des problèmes de
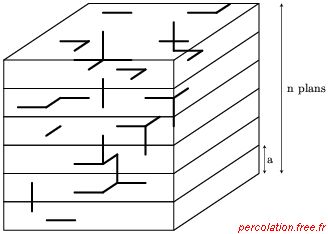
percolation en trois dimensions. La figure 2.36 (a) montre l'empilement de n
plans horizontaux de symétrie carrée et d'extension infinie, reliés les uns aux autres par des
liens verticaux de taille a.
Figure 2.36: Système d'épaisseur d par empilement de n plans horizontaux
| (a) Décomposition du système en cubes |
|
(b) Cube d'arête d = n × a |
 |
|
 |
| Source : Clerc et alii (1983), p. 77 |
Cette structure peut alors s'interpréter comme un système d'épaisseur finie d, avec
d = n × a (Clerc et alii, 1983, p. 76). La figure 2.36 (b)
montre l'agrandissement d'un des cubes composant le système. Soit p^ la
probabilité d'activité des liens sur les plans horizontaux et p// celle des liens
verticaux entre les plans adjacents. Deux situations particulières peuvent être mises en
évidence :
-
si le rapport R = p// / p^ = 1 est vérifié, le système est isotrope, car les
probabilités sont identiques. Si le nombre n de plans empilés est infini, l'ensemble
est de dimension trois et son seuil de percolation est celui du réseau cubique simple :
~ 0,24736. Si l'épaisseur du système est finie (1/n ¹ 0),
il se comporte au voisinage du seuil, comme un réseau en deux dimensions avec un effet de
taille finie. La valeur du seuil critique est alors plus faible que celle du simple
réseau carré de liens ;
- si R = p// / p^ = 0 et que le nombre de plans empilés est
infini, le système est anisotrope. La probabilité d'existence des liens verticaux étant nulle, les diverses couches
sont séparées les unes des autres. Le seuil de percolation de chacun des plans est pc = 1/2. Lorsque p^ est
inférieur à cette valeur, les amas sur chaque plan sont de taille finie. Si l'on suppose à présent que R est non nul,
la présence de liens verticaux admet l'apparition d'un chemin de liens actifs à travers le système, même si chaque plan
n'est pas percolant individuellement. Le seuil de percolation du système formé par l'empilement des plans est ainsi
plus faible que celui de chacun des plans.
Ces trois exemples de percolation anisotrope montrent comment en ajoutant une contrainte
directionnelle sur la probabilité d'activité des liens, il est possible d'enrichir la problématique
étudiée. Les modèles de percolation dirigée sont des modèles de percolation anisotrope dans le sens
où ils impliquent une contrainte directionnelle. Cependant, à la différence des exemples présentés
ci-dessus, la contrainte ne s'applique pas sur la probabilité d'activité des liens mais sur leur
orientation.
Les modèles de percolation dirigée
Selon la forme prise par la contrainte directionnelle, plusieurs modèles de percolation dirigée
peuvent s'envisager.
Lorqu'il est évoqué sans précision supplémentaire, le modèle de « percolation dirigée »
fait généralement référence au problème de percolation « entièrement dirigée »
(Fully directed). Il consiste à donner une orientation précise aux liens
présents sur le réseau, les liens parallèles étant orientés dans la même direction. Le
déplacement à travers chaque lien de ce réseau aléatoire n'est alors possible que dans le
sens indiqué. Autrement dit, les liens d'un modèle de percolation entièrement dirigée
sont actifs avec une probabilité p et orientés dans une direction déterminée selon leur
inclinaison. La figure 2.37 illustre deux exemples de réseau carré de
percolation entièrement dirigée.
Figure 2.37: Exemples de percolation entièrement dirigée sur un réseau carré
| (a) Axe de développement diagonal (nord-est) |
|
(b) Axe de développement vertical (bas) |
 |
|
 |
| Source : Grimmett (1989), p. 264 |
|
Source : Kinzel (1983), p. 428 |
Sur la figure (a), les liens horizontaux présents sont orientés vers la droite et les
liens verticaux vers le haut. Par conséquent, le développement des amas s'effectue
suivant la diagonale dans la direction nord-est. Sur la figure (b), l'axe de
développement des amas est la verticale orientée vers le bas. Dans les deux cas, le
développement des amas est anisotrope.
En électronique, ce modèle de percolation est représenté par un réseau aléatoire de transistors ou
de diodes, car le courant ne peut les traverser que dans une seule direction (Lesne, 1996, p. 316).
De façon plus précise, les diodes sont présentes avec une probabilité p et leur orientation suit
les directions +x, +y, +z, etc., sur le réseau (Redner, 1983, p. 450). Le modèle de
percolation entièrement dirigée s'applique aussi à la propagation d'une maladie dans un verger,
lorsque le vent souffle dans une direction précise (Kinzel, 1983, p. 427). Dans ce cas, l'épidémie
ne peut se propager que dans le sens du vent. Ici et contrairement aux diodes, l'orientation sur le
réseau ne tient alors pas aux liens de façon intrinsèque, mais elle résulte du champ de force
extérieur créé par le vent.
Le modèle de percolation « partiellement dirigée » (partially directed)
fonctionne selon le même principe que le précédent, mais les liens ne sont pas tous
orientés. Dans un réseau carré par exemple, les liens verticaux sont orientés vers le
haut mais les liens horizontaux ne sont pas orientés
(figure 2.38 (a)).
Figure 2.38: Autres modèles de percolation dirigée sur un réseau carré
| (a) Percolation partiellement dirigée |
|
(b) Percolation dirigée et aléatoire |
 |
|
 |
Le système est alors isotrope par rapport à l'axe horizontal, mais globalement il est
anisotrope puisqu'il est orienté dans au moins une direction. C'est par exemple le cas
d'un réseau électronique où sur les p % de liens présents, sont placés verticalement
des diodes (passage unilatéral) et horizontalement des résistances (passage bilatéral)
(Redner, 1983, p. 450).
Enfin, on peut également envisager un modèle où il n'existe pas d'axe principal de
développement et où, par conséquent, l'orientation des liens est stochastique
(figure 2.38 (b)). Dans ce modèle de percolation « dirigée et
aléatoire », le hasard agit ainsi à deux niveaux. L'activité des liens est dans un
premier temps tirée au sort. Dans un deuxième temps, c'est le sens de passage à travers
le lien qui est déterminé de façon aléatoire. Si l'orientation des liens dans un sens ou
l'autre est équiprobable, et puisqu'il n'existe pas d'axe de développement particulier,
le système est isotrope.
Seuil de percolation et exposants critiques
Le modèle de percolation (entièrement) dirigée induit une anisotropie macroscopique. Pour
caractériser le système, il est alors nécessaire d'utiliser deux longueurs de corrélation (Sahimi,
1994, pp. 115-116). La première ( x// ), est la longueur de corrélation longitudinale,
parallèle à la direction de l'axe de développement. La seconde ( x^ ), est la longueur de
corrélation transversale, perpendiculaire à l'axe de développement.
(figure 2.39).
Figure 2.39: Longueurs de corrélation longitudinale et transversale
 |
| Source : Kinzel (1983), p. 430 |
Soit pcD la valeur du seuil critique dans le modèle de percolation dirigée.
Lorsque la proportion de liens présents est inférieure à pcD, les amas du système
sont de taille finie, alors que si p > pcD, il existe un amas infini. Le fait que
les liens soient orientés rend la traversée du système plus difficile. Même si un amas de
liens actifs existe entre les deux bords d'un réseau, il est possible que l'orientation
des liens empêche sa traversée (Bunde et Havlin, 1991, p. 82). Dans ce cas, il n'y a pas
percolation du système au sens du modèle dirigé, c'est-à-dire une suite de liens orientés
formant un chemin continu et cohérent. Par conséquent, la valeur des seuils critiques est
plus élevée que dans le modèle ordinaire. Le tableau 2.3 reprend
les estimations de la valeur du seuil de percolation pour divers réseaux.
Table 2.3: Valeurs du seuil dans le modèle de percolation dirigée
| Réseau |
pcD : seuil |
| Carré de liens |
0,6445 ± 0,0005 |
| Carré de sites |
0,7058 ± 0,0005 |
| Triangulaire de liens |
0,479 ± 0,003 |
| Cubique simple |
0,383 ± 0,003 |
| Cubique centré |
0,287 ± 0,003 |
| Cubique faces centrées |
0,199 ± 0,003 |
| Source : Kinzel (1983), p. 436 |
Au voisinage du seuil, l'évolution des longueurs de corrélations longitudinale et transversale
s'effectue suivant les lois d'échelle (Kinzel, 1983, p. 427) :
|
|
| x// » | p – pcD |– n// |
et |
x^ » | p – pcD |– n^ |
|
(20) |
Table 2.4: Valeurs des exposants universels pour le modèle de percolation dirigée
|
| Exposant |
d = 2 |
d = 3 |
d = 4 |
d = 5 – e |
|
| b |
0,280 ± 0,01 |
0,600 ± 0,005 |
|
1 – (e /6) |
| g |
2,280 ± 0,01 |
1,580 ± 0,02 |
1,230 ± 0,005 |
1 + (e /6) |
| n// |
1,734 ± 0,002 |
1,270 ± 0,01 |
|
1 + (e /12) |
| n^ |
1,100 ± 0,005 |
0,735 ± 0,015 |
|
(1/2) + (e/16) |
| s |
0,390 |
0,460 |
|
1 + 0(e2) |
| t |
2,112 ± 0,005 |
2,280 |
|
3 – (e/6) |
|
| Source : Kinzel (1983), p. 438 |
À travers le modèle de percolation dirigée, une nouvelle hypothèse de base du modèle ordinaire a été relâchée. Les
liens étant orientés, un axe principal de développement apparaît. De même que lorsque les probabilités d'activité sont
différentes selon la direction des liens, le système se montre alors macroscopiquement anisotrope. En conséquence, les
grandeurs caractéristiques du problème évoluent de façon spécifique ce qui donne naissance à une classe d'universalité
différente de celle du modèle basique. Dans le paragraphe suivant, la remise en cause d'une autre hypothèse de base est
discutée : l'indépendance statistique de l'état des éléments.
2.3.3 Percolation corrélée
Le modèle basique de percolation postule que l'état (actif ou inactif) d'un élément est
déterminé de façon aléatoire et non corrélée avec celui des autres éléments du système.
Dans le modèle de percolation de sites par exemple, l'activité d'un site est
statistiquement indépendante de l'activité des autres sites. Lorsque l'on suppose
l'inverse, le problème correspond alors au modèle de percolation corrélée. En référence à
la variable et à la loi de Bernoulli, le problème ordinaire de percolation où les
éléments sont indépendants est appelé modèle de percolation de Bernoulli (Kesten, 1987,
p. 1237). Dans le même sens, le modèle de percolation corrélée est également qualifié de
percolation « non-Bernoulli ».
Il existe deux façons de faire intervenir la corrélation dans un problème de percolation : soit par une interaction
entre les éléments, soit en introduisant des corrélations sur les propriétés des éléments (Ramirez-Cuesta et
alii, 1998, p. 2). Les deux premiers points de ce paragraphe s'intéressent à l'interaction des éléments et le dernier
montre un exemple de corrélation des propriétés des éléments. Ainsi, après avoir évoqué la notion de champ aléatoire de
Markov et de modèle d'Ising, nous présenterons un modèle de percolation où l'activité d'un site dépend de l'état de son
environnement. Un modèle de corrélation entre les sites et les liens sera enfin évoqué.
Champ aléatoire de Markov et modèle d'Ising
La notion de champ aléatoire de Markov est fondée sur le principe selon lequel
l'état d'un élément dépend de celui de son environnement (Hammersley et Mazzarino,
1983-a, p. 205). La théorie des champs markoviens vient de la physique. Elle correspond à
une généralisation du processus de Markov où la dimension temporelle est remplacée par
l'indexation spatiale (Kindermann et Snell, 1980-b, p. 1). La motivation initiale du
concept de champ de Markov est d'apporter un cadre formel au modèle d'Ising. Ce
modèle, du nom de son auteur le physicien allemand E. ISING, analyse le comportement d'un
système ferromagnétique37.
La formulation la plus simple du modèle d'Ising s'effectue sur un segment. Les éléments du système
y sont placés à intervalle régulier. Chacun de ces éléments possède une orientation parmi deux
possibles : haut ou bas. Dans un problème ferromagnétique, cette orientation correspond au
spin, c'est-à-dire à la nature du moment magnétique de la particule : positive ou
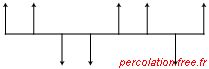
négative. La figure 2.40, montre un exemple d'orientation des spins dans un modèle
en dimension un.
Figure 2.40: Exemple d'orientation des spins dans un modèle d'Ising en dimension un
 |
| Source : Kindermann et Snell (1980-b), p. 2 |
L'objectif du modèle d'Ising est de déterminer une mesure de probabilité sur
l'espace W de l'ensemble des séquences possibles. Chaque configuration w =
(w0, w1, ..., wn) est définie comme une séquence
particulière de signes « + » et « – », les premiers s'associant aux spins dirigés
vers le haut et les seconds aux spins dirigés vers le bas38.
Chaque spin est supposé de module | sj | = 1. Dans ces
conditions, le spin prend la valeur 1, lorsque wj = « + » et – 1, lorsque
wj = « – ». À chaque configuration w, on associe une énergie U(w)
de la forme (Kindermann et Snell, 1980-b, p. 2) :
|
U(w) = – J |
|
si(w) sj(w) – mH |
|
si
(w)
(21) |
Le modèle d'Ising associe à chaque configuration w, une probabilité proportionnelle à
e– 1/kT U(w). La mesure de probabilité sur l'espace W se définit alors par
:
où la constante Z est appelée « fonction de partition ». Ce type de mesure déterminée
par une fonction d'énergie U, correspond à une mesure de
Gibbs. Celle-ci possède la propriété (Kindermann et Snell, 1980-b,
p. 6) :
P(
sj =
a |
sk,
k ¹ j) =
P(
sj =
a |
sk,
k Î Nj)
(23)
où Nj correspond à l'ensemble des sites plus proches voisins de j. La
relation (23) signifie que la probabilité du spin au point j, la
valeur de tous les autres spins du système étant donnée, est égale à la probabilité du
spin au point j lorsque seule la valeur des spins plus proches voisins de j est
donnée. En d'autres termes, l'état d'un spin ne dépend que de celui de ses plus proches
voisins. Lorsqu'une mesure vérifie cette relation, elle est appelée « champ aléatoire de
Markov ».
Pour résumer le mécanisme du modèle d'Ising, l'état initial du système est formé par une
distribution aléatoire de spins orientés vers le haut ou le bas. Les interactions
conduisent à une configuration d'état énergétique plus faible. Lorsque J est positif,
l'énergie entre les paires de spins est plus faible, s'ils sont orientés dans la même
direction. Lorsque J est négatif, l'énergie entre les spins est plus faible, s'ils sont
dans des directions opposées. Après un certain temps de relaxation, le système se
stabilise. À l'équilibre, la nature magnétique du matériau se détermine alors par la
différence du nombre n+ (w) de spins orientés vers le haut et n– (w)
orientés vers le bas. La même analyse peut être reproduite dans des dimensions
supérieures. Dans un réseau carré par exemple (d = 2), l'énergie de chaque configuration
est calculée selon (21), et la mesure de probabilité est définie par
(22)39 (Kindermann et
Snell, 1980-b, p. 4).
Percolation-éviction et percolation-diffusion
D'une façon voisine de celle décrite précédemment, un modèle modifie le comportement des
sites en fonction de la structure de leur entourage. Le réseau initial est formé, comme
dans le modèle basique de percolation, par un ensemble de sites dont l'activité est
aléatoire. Chaque site du réseau est actif avec une probabilité p ou inactif avec une
probabilité (1 – p). Dans un deuxième temps, l'état de certains sites évolue selon leur
voisinage. Deux sous-modèles se distinguent (Chaves et Koiller, 1995, p. 272) : la «
percolation-éviction » (bootstrap percolation) et la « percolation-diffusion »
(diffusion percolation).
Dans le modèle de percolation-éviction, les sites actifs ayant moins de l sites actifs,
parmi leurs plus proches voisins, sont transformés en sites inactifs. Cette opération d'éviction se
poursuit jusqu'à ce que tous les sites actifs aient au moins l plus proches voisins actifs ou
lorsque tous les sites sont inactifs. Ce modèle s'associe par exemple au comportement d'aimantation
d'un système dilué. Un atome y manifeste un moment magnétique, uniquement si un nombre suffisant de
ses voisins sont eux même aimantés. Le seuil de percolation pcBP (l) est la valeur de p à
partir de laquelle un amas infini existe encore après la procédure d'éviction.
Dans le modèle de percolation-diffusion, les sites inactifs ayant au moins k sites
actifs plus proches voisins sont eux même transformés en sites actifs. Cette opération d'activation
est réitérée jusqu'à ce que tous les sites inactifs aient moins de k sites actifs dans leur plus
proche voisinage ou lorsque tous les sites sont actifs. Ce processus est typique de la propagation
d'un fluide dans un milieu poreux. Un site a de fortes chances d'être atteint par le fluide lorsque
son voisinage est déjà touché. Le seuil de percolation pcDP (k) est la valeur de p à partir
de laquelle un amas infini apparaît à la fin du processus de diffusion.
Pour une valeur précise des paramètres k et l, les seuils de percolation sont identiques à
celui du modèle basique de percolation de site (Medeiros et Chaves, 1997, p. 604) :
pcBP (0) = pcDP (z + 1) = pc
(24)
où z correspond à la coordinence du réseau, c'est-à-dire au nombre de plus proches voisins d'un site. Le modèle
d'éviction qui supprime un site actif lorsque celui-ci a moins de l = 0 plus proches voisins actifs, n'engendre aucune
modification du système initial. Aucun élément ne peut être encadré par moins de zéro sites actifs40. De même, le modèle de
diffusion qui active un site lorsque celui-ci a au moins k = z + 1 sites actifs dans son entourage est invariable. Aucun
élément ne peut être encadré par plus de z sites actifs41. Les deux modèles de percolation
corrélée ont alors un comportement semblable à celui du modèle standard de percolation de sites.
De façon plus générale, on peut formuler pour un réseau donné, une comparaison de la valeur du
seuil de percolation de ces trois modèles :
pcDP (k) £ pc £ pcBP (l)
(25)
Intuitivement, il apparaît en effet plus simple d'obtenir un amas infini de sites actifs dans le
processus de percolation-diffusion, que dans le modèle basique de percolation qui, à son tour, se
montre plus simple que le modèle de percolation-éviction. Ceci se vérifie empiriquement par des
simulations numériques. Les estimations de la valeur du seuil de percolation pour différents
réseaux, sont reprises dans le tableau 2.5.
Table 2.5: Valeurs du seuil dans le modèle de percolation corrélée
| Réseau (sites) |
pcBP (l) : ÉVICTION |
pcDP (k) : DIFFUSION |
| Nid d'abeille1 |
l = 1 |
0,6970 ± 0,0005 |
k = 3 |
0,5598 ± 0,0005 |
| |
l = 2 |
0,6972 ± 0,0001 |
k = 2 |
0,3096 ± 0,0003 |
| Carré1 |
l = 1 |
0,5931 ± 0,0005 |
k = 4 |
0,5471 ± 0,0005 |
| |
l = 2 |
0,5925 ± 0,0005 |
k = 3 |
0,4196 ± 0,0005 |
| Triangulaire2 |
l = 2 |
0,4997 ± 0,0005 |
k = 5 |
0,5000 ± 0,0005 |
| |
l = 3 |
0,6291 ± 0,0005 |
k = 4 |
0,3708 ± 0,0005 |
| Sources : (1) Chaves et Koiller (1995), p. 276 ;
(2) Medeiros et Chaves (1997), p. 608 |
Au passage, on notera que les tests sur les exposants critiques mettent en évidence un
comportement universel pour le modèle de percolation-éviction comme pour le modèle de
percolation-diffusion42.
Percolation corrélée sites-liens
Un autre type de problème de percolation corrélée consiste à introduire des corrélations
statistiques entre les propriétés des éléments d'un système. Ce type de modélisation
s'associe notamment à l'étude de surfaces hétérogènes et de milieux poreux. C'est le cas,
par exemple, dans un modèle de percolation mixte lorsque les sites sont associés à des «
cavités » (de tailles diverses), les liens à des « artères » (de tailles diverses), et
que leurs rayons respectifs sont corrélés.
Soit rs le rayon des cavités (sites) et rb le rayon des z artères (liens) qui y sont attachées. Le désordre est
introduit dans le système à travers ces deux variables. À chacun de ces rayons est associé une fonction de densité :
fs (rs) pour les sites et fb (rb) pour les liens. Autrement dit, la probabilité pour une cavité d'avoir un
rayon compris entre r et r + dr est égale à fs (r). De même, la probabilité pour que le rayon d'une artère soit
compris entre r et r + dr est de fb (r). Les fonctions de répartition S(rs) et B(rb) associées,
respectivement, aux sites et aux liens sont définies par (Ramirez-Cuesta et alii, 1998, p. 3) :
Ces fonctions précisent la probabilité de trouver une cavité ou une artère de rayon inférieur ou
égal à rs.
Un « principe de construction » doit être pris en compte dans la modélisation, afin que
le système reste cohérent : la taille d'un site donné doit toujours être supérieure à
celle de ses liens (Vidales et alii, 1995, p. 20). Cette propriété est toujours
vérifiée lorsque les fonctions fs et fb sont telles que les surfaces situées sous
leurs courbes ne se chevauchent pas. Au contraire, lorsqu'il existe un tel chevauchement,
certains sites et certains liens ne peuvent plus être reliés. Une corrélation entre la
taille des sites et la taille des liens apparaît par conséquent. Cette corrélation se
décrit par une fonction de densité sites-liens (fsb) définie telle que
(Ramirez-Cuesta et alii, 1998, p. 3) :
fsb (rs, rb) = fs (rs) fb(rb) f (rs, rb)
(27)
où f désigne une fonction de corrélation sites-liens caractérisant la structure. Lorsque f
= 1, les sites et les liens ne sont pas corrélés. Toute autre valeur de f indique qu'il existe
un certain degré de corrélation. De manière générale, f se définit par :
|
|
ì
ï
ï
í
ï
ï
î |
| f (rs, rb) |
= |
| exp |
æ
ç
ç
ç
ç
è |
ó
õ |
|
|
|
|
ö
÷
÷
÷
÷
ø |
|
|
| B(rs) – S(rs) |
|
si |
rs ³ rb |
| f (rs, rb) |
= |
0 |
si |
rs < rb |
|
|
(28) |
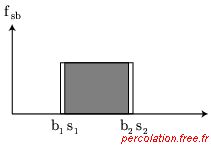
Soit W le degré de chevauchement des surfaces situées sous les courbes des deux fonctions de
densité fs et fb. Sur la figure 2.41, la distribution des rayons pour les
sites et les liens est posée uniforme.
Figure 2.41: Chevauchement des distributions des rayons pour les sites et les liens
| (a) W = 0 |
(b) W » 0,5 |
(c) W » 1 |
 |
 |
 |
| Source : Vidales et alii (1995), p. 21 |
La taille du rayon d'un site est comprise entre s1 et s2 et celle d'un lien entre
b1 et b2. Dans ces conditions, moins le chevauchement est important et plus le modèle
se rapproche du problème de percolation standard, c'est-à-dire non-corrélée.
Pour ramener cette modélisation a un problème de percolation, les sites et les liens sont supposés
ouverts uniquement lorsque leurs rayons dépassent respectivement les valeurs critiques rsc
et rbc. La probabilité d'activité d'un site (ps) se détermine ensuite à partir de
rsc, par un rapport des surfaces située sous la fonction de densité fs43. De même, la probabilité d'activité d'un liens (pb) est reliée à la valeur de
rbc.
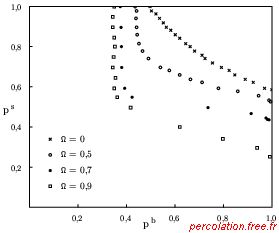
La figure 2.42 montre le résultat des simulations numériques de ce modèle
dans un réseau carré, selon le degré de chevauchement des distributions.
Figure 2.42: Ligne de transition pour le modèle de percolation mixte corrélée
 |
| Source : Vidales et alii (1995), p. 26 |
La ligne de transition représentée pour les diverses valeurs de f sépare la phase
percolante (coin nord-est) et la phase non-percolante (coin sud-ouest)44. Pour f = 0, la ligne de transition correspond à
celle du modèle de percolation mixte standard. Sur la figure 2.42,
on constate que plus la corrélation est forte entre les sites et les liens (f
® 1), plus la ligne de transition est située à gauche. La corrélation des
sites et des liens agit par conséquent, comme un élément favorable à la percolation du
système.
Durant cette même série de simulation, la probabilité de percolation des sites et des liens a été
analysée pour différentes valeurs du chevauchement. Alors que pour de faibles corrélations, la
courbe de la probabilité de percolation des sites évolue de façon monotone (comme d'ordinaire), ce
n'est plus le cas lorsque la corrélation augmente. À titre d'exemple, pour f = 0,6 la
probabilité de percolation des sites atteint un maximum (ps ~ 0,77) puis décroît. Ce
comportement atypique s'explique par la corrélation de l'activité des sites et des liens. Il se
retrouve également dans l'étude du modèle sur un réseau de Bethe (Faccio, Zgrablich et Mayagoitia,
1993, repris dans : Vidales et alii, 1995).
Dans ce paragraphe, plusieurs modèles de percolation corrélée ont été présentés, en distinguant les modèles
d'interaction entre les éléments et les modèles de corrélation entre les propriétés des éléments. Ainsi, la notion de
champ aléatoire de Markov a été présentée au travers du modèle d'Ising. Les modèles de percolation-éviction et
percolation-diffusion ont été analysés en mettant l'accent sur la valeur des seuils obtenus par simulation numérique,
dans différents réseaux. Enfin, le modèle de percolation corrélée sites-liens a mis en évidence les effets positifs de
la corrélation sur la percolation du système. L'objet du paragraphe suivant concerne à présent la modification du
réseau.
2.3.4 Modification du réseau
Tel qu'il a été défini dans le premier chapitre, le problème de percolation se pose dans un graphe,
c'est-à-dire un ensemble de sommets et d'arêtes, où deux sommets quelconques sont reliés par au
plus une arête. En conséquence, la théorie ne se limite pas aux simples réseaux symétriques. Ainsi,
après un exemple de percolation dans un réseau irrégulier, la question de la valeur de leur seuil
de percolation sera discutée au travers de la notion de quasi-invariant. L'intérêt des exposants
critiques universels sera enfin évoqué.
Réseau irrégulier
Par commodité, la plupart des systèmes de percolation sont représentés dans des réseaux
réguliers45 : réseau nid d'abeille, carré, triangulaire, cubique, etc. De
la sorte, les seuils de percolation associés sont déterminés de façon exacte ou
approchée. Le calcul de la valeur du seuil est entièrement déterminé par la structure du
graphe où évolue le problème de percolation.
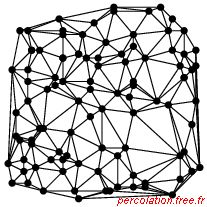
La figure 2.43 illustre un problème de percolation de sites dans un réseau
irrégulier.
Figure 2.43: Exemples de réseaux irréguliers (100 sites)
| (a) 271 liens |
|
(b) 280 liens |
 |
|
 |
Dans le cas (a) comme dans le cas (b), les réseaux sont formés par 100 sites dont l'emplacement a été fixé de façon
aléatoire. Les liens possibles entre chaque sites voisins ont été représentés de façon à ce que le graphe soit
planaire. Un graphe est planaire, lorsqu'il en existe une représentation géométrique dans le plan alors que
ses arêtes ne se coupent pas. Les sites étant placés différemment sur la figure 2.43 (a) et la
figure 2.43 (b), le nombre de liens possibles n'est pas le même : 271 dans le premier cas et 280 dans le
second.
Les figure 2.44 (a), (b) et (c) montrent respectivement une configuration de
percolation de sites, de percolation de liens et de percolation mixte, sur le réseau de la
figure 2.43 (a).
Figure 2.44: Les trois modèles classiques de percolation
| (a) Percolation de sites |
(b) Percolation de liens |
(c) Percolation mixte |
 |
 |
 |
| ps = 0,5 |
pb = 0,5 |
ps = 0,5 et pb = 0,5 |
Le paramètre ps précise le pourcentage de sites actifs et le paramètre pb celui de
liens.
Selon les mêmes règles que dans les réseaux réguliers, lorsque le niveau d'activité augmente, un
amas percolant apparaît à une valeur critique qui correspond au seuil de percolation du réseau. Il
est impossible de déterminer de façon générale la valeur exacte du seuil de percolation de
l'ensemble des réseaux irréguliers. Chaque graphe étant original, le seuil de percolation lui est
propre. Une relation entre la valeur du seuil et la coordinence peut cependant être formulée.
Seuil de percolation et quasi-invariant
La valeur des seuils de percolation du tableau 1.5
(p. ??), s'associent à la notion de quasi-invariant
(Clerc et alii, 1983, p. 66-67). Pour les réseaux ordonnés, des relations
approchées sont mises en évidence. En percolation de liens, ces relations permettent
d'associer seuil et coordinence : z pcb ~ 2 ± 0,1 en deux dimensions et z
pcb ~ 1,5 ± 0,1 en trois dimensions. La même relation n'existe pas en
percolation de sites. Il est cependant possible mais non justifié théoriquement,
d'estimer pc sur un réseau désordonné à partir de la connexité moyenne z, car les
variations de pcs et z– 1 sont monotones (figure 2.45).
Figure 2.45: Seuil de percolation de sites et coordinence pour divers réseaux
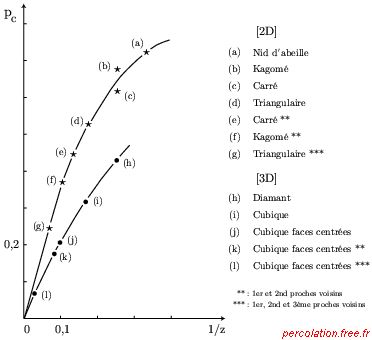 |
| Source : Clerc et alii (1983), p. 67 |
Un exemple de l'utilisation de ces relations peut être construit à partir
d'une distribution quelconque de points dans le plan. Une tesselation est alors effectuée,
c'est-à-dire un dallage du plan par des polygones de Voronoï46. Un polygone de Voronoï représente la
surface la plus petite pouvant être construite autour d'un point, à partir des médiatrices des
segments le liant aux autres points (figure 2.46).
Figure 2.46: Tesselation d'un plan par des polygones de Voronoï
 |
| Source : adapté de Clerc et alii (1983), p. 66 |
Le nombre moyen de faces des polygones correspond pour un site, au nombre moyen de ses
voisins. La coordinence du réseau représenté par la figure 2.46 est z =
6. Par conséquent, le seuil de percolation est proche de celui du réseau triangulaire de
sites. Les simulations effectuées confirment le résultat puisque le seuil est estimé aux
alentours de 1/2 (Winterfeld, Scriven et Davis, 1981, repris dans : Clerc et
alii, 1983, p. 66).
Dans des travaux récents, S. GALAM et A. MAUGER proposent une formule universelle pour
l'approximation des seuils de percolation (Galam et Mauger, 1996 et 1997). Cette
relation, mise en évidence pour les modèles de percolation de sites et de liens, se
traduit par :
|
pcs = p0 [ (d – 1)(z – 1) ]– a et pcb = p0 |
é
ê
ê
ë |
|
|
ù
ú
ú
û |
|
Exposants critiques universels
Au voisinage du seuil critique, la plupart des grandeurs statiques du modèle de percolation ont un
comportement qui est indépendant de la structure du réseau et des détails microscopiques du
système47. Les lois d'échelle décrivent ces comportements et
un exposant critique est associé à chacune d'elle. Ces exposants sont reliés les uns aux autres et
ils ont également la propriété d'être universels. Autrement dit, pour un modèle de percolation
donné et dans un problème de même dimension, la valeur des exposants critiques est identique quelle
que soit la forme du réseau. Ces exposants définissent ainsi des classes d'universalité.
Le tableau 1.8 (p. ??) précise les valeurs
des exposants critiques pour le modèle de percolation basique, c'est-à-dire lorsque l'activité d'un
site est aléatoire et indépendante de celle des autres sites. Pour la dimension d = 2 par exemple,
l'exposant qui est associé à la taille moyenne des amas finis S(p) est : g = 43/18. Au
voisinage du seuil de percolation, S(p) suit une évolution identique dans un réseau nid
d'abeille, un réseau carré ou un réseau triangulaire48 :
Le seuil de percolation est différent dans chacun de ces réseaux, mais dans son voisinage, le
comportement du modèle est identique. Cette universalité s'applique également aux réseaux
irréguliers. Ainsi, un problème de percolation dans une structure du type de la
figure 2.43, dont l'activité de chaque site est aléatoire et indépendante de celle
des autres sites, évolue avec les mêmes exposants que ceux du tableau 1.8,
au voisinage de son seuil de percolation. Cette propriété est fondamentale, car elle montre
l'intérêt de l'analyse de réseaux réguliers pour obtenir des informations sur le comportement du
système, ces informations pouvant ensuite s'appliquer à des réseaux de formes irrégulières.
Cette section a présenté les principaux modèles de percolation résultant de la déformation du modèle basique de
percolation. Ces modifications se sont tout d'abord portées sur la notion de voisinage, où plusieurs définitions
différentes de l'entourage d'un site ont été présentées (von Neumann, Moore et Moore-von Neumann). Les conséquences du
voisinage sur la valeur du seuil de percolation ont alors été soulignées. La non-orientation des éléments du système a
ensuite été remise en cause avec le concept de percolation anisotrope et le modèle de percolation dirigée. À son tour,
l'indépendance de l'état d'un élément, par rapport à celui d'autres éléments du système, a été discutée avec les
modèles de percolation corrélée. Le modèle d'Ising et la notion de champ aléatoire de Markov ont alors été présentés,
suivis par les modèles de percolation-éviction et percolation-diffusion, ainsi que de percolation corrélée sites-liens.
Enfin, le modèle basique de percolation a été exposé dans le cadre des réseaux irréguliers. Toutes ces extensions ne
sont que quelques unes des modifications pouvant s'envisager à partir du modèle simple décrit dans le premier chapitre.
La seule combinaison de ces diverses déformations engendrerait des modèles encore plus complexes. La théorie de la
percolation ne se limite cependant pas à ces modèles. La section suivante évoque d'autres modélisations fondées sur le
concept de percolation.








